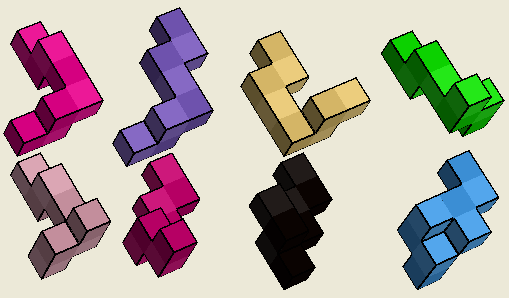I've made many polycube puzzles out of several different media.
Almost all are designs I've wanted to try but where I could not find or purchase the original.
I am not a skilled woodworker, so my preferred media are Lego and LiveCube.
I have made a few puzzles from wood:
| |
Coffin's 3-piece pyramid
|
The Bedlam Cube
|
|
I have made several puzzles from Lego (I posted some photos on Brickshelf).
The challenge is structuring the Lego bricks such that the forces encountered while manipulating
the puzzle pieces will not tend to break the Lego bonds
(this assumes you don't want to commit the pieces by gluing them together).
I was inspired by a confluence of 4 factors:
Here are the results so far:
I have made several cubes from LiveCube (most have since been recycled):
|
3x3x3
|
Nob's Cube (in Holmes' Compendium)
|
Macaroni by Kohfuh Satoh
|
Mikusinski Cube
|
Cube Conundrum from houseofmarbles.com (no longer available)
|
Osa's Cube -
I found this difficult, even after solving it several times!
|
construct a 3x3x6 tower using nine pieces
|
|
|
|
|
|
|
|
|
|
4x4x4
|
William Waite's Allsides Cube
|
Albert Gubeli's Carralbi Cube
|
Calmplex Cube
|
Yachimata Cube
By Ishino
|
Coffin's
Convolution
- even though a "rotation" is required, the LiveCube version works fine.
|
Minh Shih's Padlock Cube
- very similar to Convolution, but with more rotation!
|
Trevor Wood's
Holey Squares
(including stand!)
|
Mayer's Cube No. 3 (Model 10C) - see "A Compendium of Cube-Assembly Puzzles using Polycube Shapes" p 4^3-57.
NOTE that there is an error - one of the pieces should have only 10 units, not 11 (there is no F shaped face)
|
One in a Trillion
|
Owen's Cross
(assemble into a 4x4x3 plus sign)
|
|
|
|
|
|
|
|
5x5x5
|
Inspired by reading about Happy Cubes (Wirrel Warrel) in
a back-issue of the CFF newsletter - Issue #50 Oct. 1999, Part 4/6 -
and following information on
Jurgen Koeller's Happy Cubes page,
I made my own set of generic pieces from LiveCube.
I used 8 cubes each for the 6 centers (in black) and an additional total of 44 yellow cubes to be distributed
about the edges, as required by the various piece configurations.
|
Rick Eason's "Twenty" Cube
Here are the
specs on Puzzle Will Be Played.
|
|
|
Entrelacs -
Defi Jeu
The ten digits 0-9 in 1x3x5 cubie format, plus 6 other pieces, form a 5x5x5 cube.
|
|
Other Designs Using LiveCube
I found a description of the "New L-Square" puzzle in Edward Hordern's "What's Up" column in the CCF newsletter
issue #51 Feb. 2000, on page 30. I made pieces from LiveCube, and since one is prohibited from flipping the pieces,
I left studs showing - the pieces must remain studs up. Form a square from the pieces.
I have also made burrs from LiveCube:
Roever's Uncoated Burr (IPP 25)
These look like burrs but aren't:
The Stegmann Two-Ns Cube No. 1
Conceived Nov. 28, 2003
See it on Ishino's site.
- 8 pcs, 8 unit cubes each
- each piece is made from two joined N-tetrominoes (hence the Two-Ns, like my last name!)
- there are 4 pairs of two identical pieces:
a=h, b=g, c=f, d=e
- All 8 pieces interlock to form a 4x4x4 solid cube (no voids)
I would rate the 2 N's Cube of medium difficulty - it shouldn't take long for an experienced metagrobologist to solve it,
but I think it presents a good challenge for the casual puzzler, particularly if one starts
with it disassembled and hasn't seen the assembled arrangement.
The design is the product of a search "by hand" (i.e. without a computer) for a selection of non-planar pieces formed from
two n-tetrominoes each that would allow interlocking assembly into a 4x4x4 cube.
My "theme" was the frequent mis-spelling of my last name, which has two n's.
I was pleased to discover an arrangement that used four pairs of pieces - thusly again doubling the double-n theme - and yet
assembled in a way that was not completely symmetric.
Top Layer Bottom Layer
a b b c e e b b d e e f h h e e
a a c c d e e b d d f f g h h h
d a c b d c c b g d f h g f f h
d a a b c c a a g g g h f f g g
Scott T. Peterson is a talented craftsman from the state of Washington, who produces high-quality limited editions of
puzzles in fine woods. He and I have been corresponding, and Scott has
made a few instances of my
2 N's Cube design.
Scott has devised an attractive coloring scheme for the cube and made me the examples shown below -
the first in Bocote and Yellowheart, and the second in Kingwood and Holly.
For those of you who have been wondering, yes, I did name my first design the #1 because I intended to
continue to look for other designs using the same theme.
Well, after quite a hiatus (has it really been almost four years???), I finally spent some time on that project
in early July 2007.
However, this go-around I employed my computer to help search for good candidates.
I also made use of
Andreas Roever's amazing program BurrTools.
First, I wanted to figure out how many different candidate pieces exist.
Polycube pieces composed of eight cubes are called octocubes, and
while writing
my section on polyforms,
I learned that there are 6922 octocubes including mirror images.
That is a lot of pieces to consider, so I narrowed it down to non-planar pieces that fit in a 4x4x4 volume,
composed of two N-tetrominoes.
I enumerated them by hand, entering them into BurrTools.
BurrTools was able to eliminate inadvertent duplicates and indicate mirror image pairs.
If I've done it correctly, there are 86 pieces that meet my criteria - 40 chiral and 6 achiral.
After an initial run to search for assemblies using all 86 pieces,
I chose 22 pieces to eliminate from consideration, based on noticing that using those pieces resulted in
uninteresting, non-interlocking, "loose" assemblies, and re-ran, allowing a maximum of two copies (minimum zero)
of any of the remaining 64 to be used in an assembly.
Here are the 64 pieces:
The results?
Using an Intel P4 @ 2.8GHz with 1.5GB of RAM, BurrTools ran for 14.3 hours and found 950 assemblies, among which there
were 57 solutions, including my original 2-N's Number 1.
I inspected all the solutions, looking for assemblies that interlocked in some way - most of the solutions
were very loose and many were composed of equal halves.
I've selected a few assemblies that I thought were interesting - they are now the 2-N's Cubes numbers
2, 3, 4, and 5 and are described below.
Among the assemblies that used four pairs of pieces, I really couldn't find anything that interlocked better than
the design I had already come up with by hand!
Designs numbers 2, 3, and 4 are variations on my No. 1.
Design No. 5 is my favorite among these new ones, but uses eight distinct pieces.
- No. 1: 2 each of 0, 11, 30, and 60
- No. 2: 2 each of 1, 7, 11, and 30
- No. 3: 2 each of 0, 1, 30, and 44
- No. 4: 2 each of 0 and 44, and 1 each of 1, 11, 30, and 60
- No. 5: 1 each of 0, 1, 3, 7, 13, 26, 30, and 36
The Stegmann Two-Ns Cube No. 2
Conceived July 2007
Like No. 1, this one uses pairs of four different piece types, two of which have appeared in #1 and two of which are new.
Two of the piece types are mirror images of one another.
The structure is very similar to #1.
b b e e e b b d a a c c f c c h
e e e d e f b d f a a a f c h h
e d d d f f b b f g g a c c h a
d d g g f g g b g g h h c h h a
The Stegmann Two-Ns Cube No. 3
Conceived July 2007
Again, pairs of four different piece types - two types appearing in #1, one from #2, and a new one.
Another variant of #1, but looser.
d b b g e e b b h c c c c c a a
d b e g d e e g h h g c a a a c
b b e e d f f g a h g g a h h c
b d d e d d f f a f f g f f h h
The Stegmann Two-Ns Cube No. 4
Conceived July 2007
A hybrid of #1 and #3.
d e e g e e b b h c c c c c a a
d b e g d b b g h h g c a a a c
b b e e d f f g a h g g a h h c
b d d e d d f f a f f g f f h h
The Stegmann Two-Ns Cube No. 5
Conceived July 2007
This one uses eight different pieces.
It holds together pretty well.
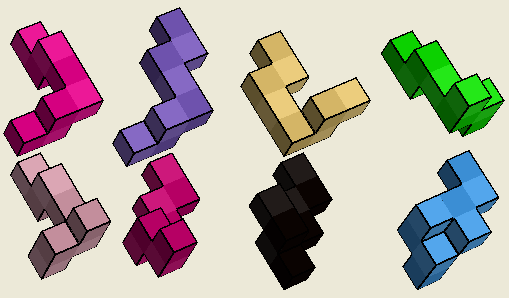
g g h h h g g e a a g g c a a b
h h h e h f f e f g g b c c a b
h d d e f f c c f c c b f c a a
d d e e d e e b d d b b f d b a
