Rearrangement / Permutation

his section is devoted to puzzles having similar pieces which must be re-arranged, or permuted, often as groups, in order to progress from a randomized (mixed or scrambled) state to a solved state. This group forms a sub-class of the Sequential Movement puzzles. The "Twisty Polyhedra" comprise a large and growing sub-class. Many of these puzzles are mass-produced (or hand-crafted modifications to a mass-produced puzzle), colorful, and made of plastic. Every puzzler knows about Rubik's Cube, the quintessential representative of this group. These puzzles are in the form of a Platonic or an Archimedean solid, "sliced" along various planes to permit certain axes of rotation of pieces or groups of pieces. They contain clever internal mechanisms which keep the moving pieces coherent. (You can see many patents showing the mechanisms at Joshua Bell's site.) A lot of group-theory mathematics applies to this category. Useful sequences of moves are known as "operators" or "algorithms."

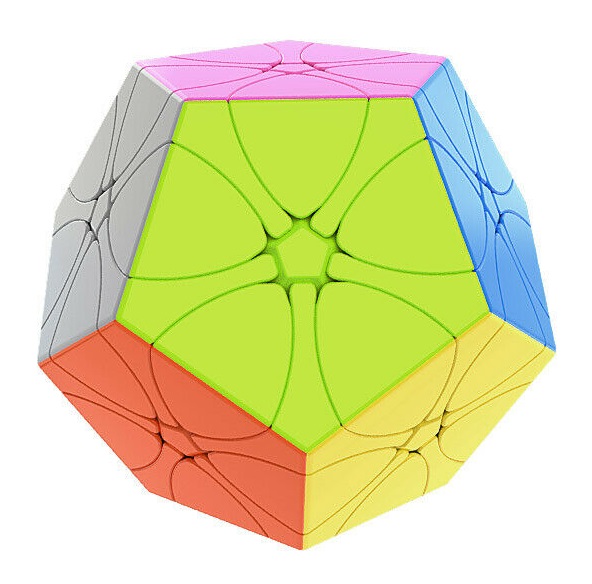
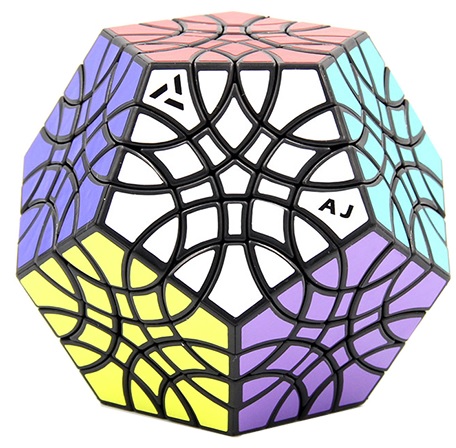
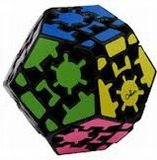
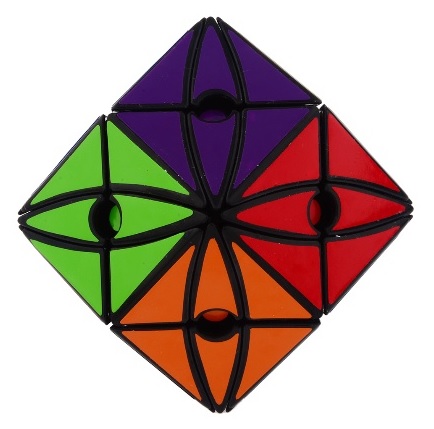
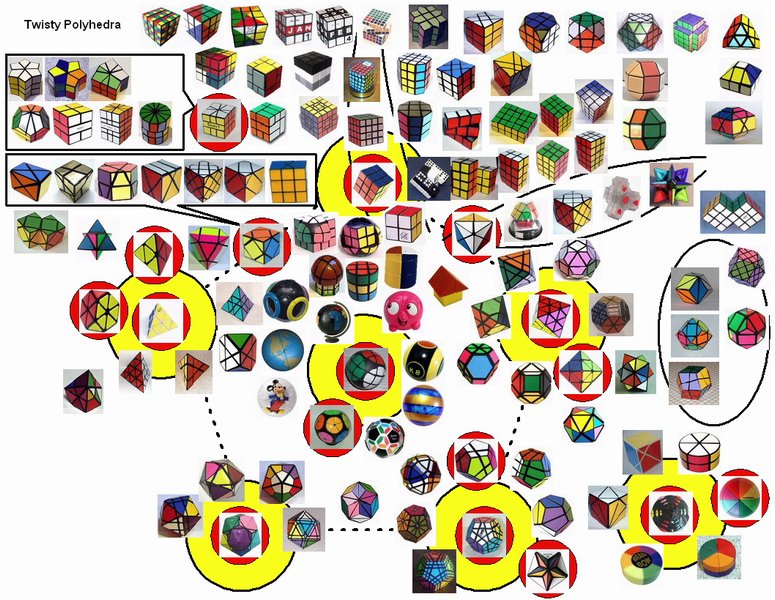
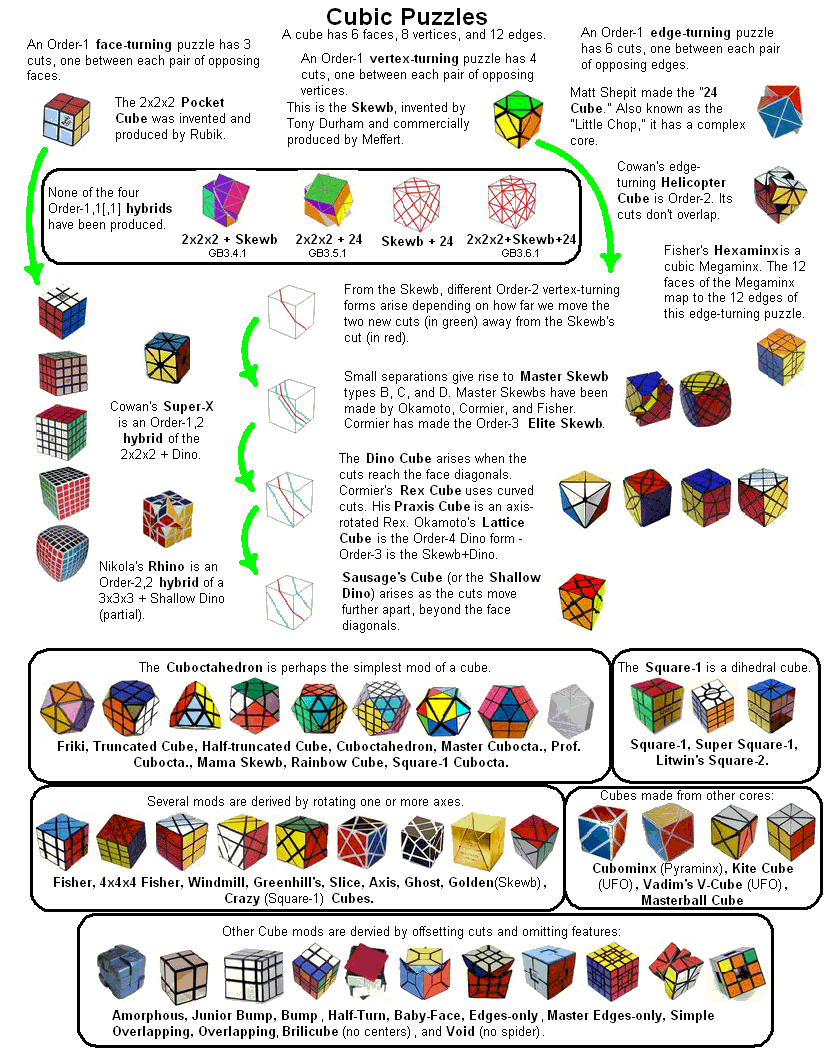
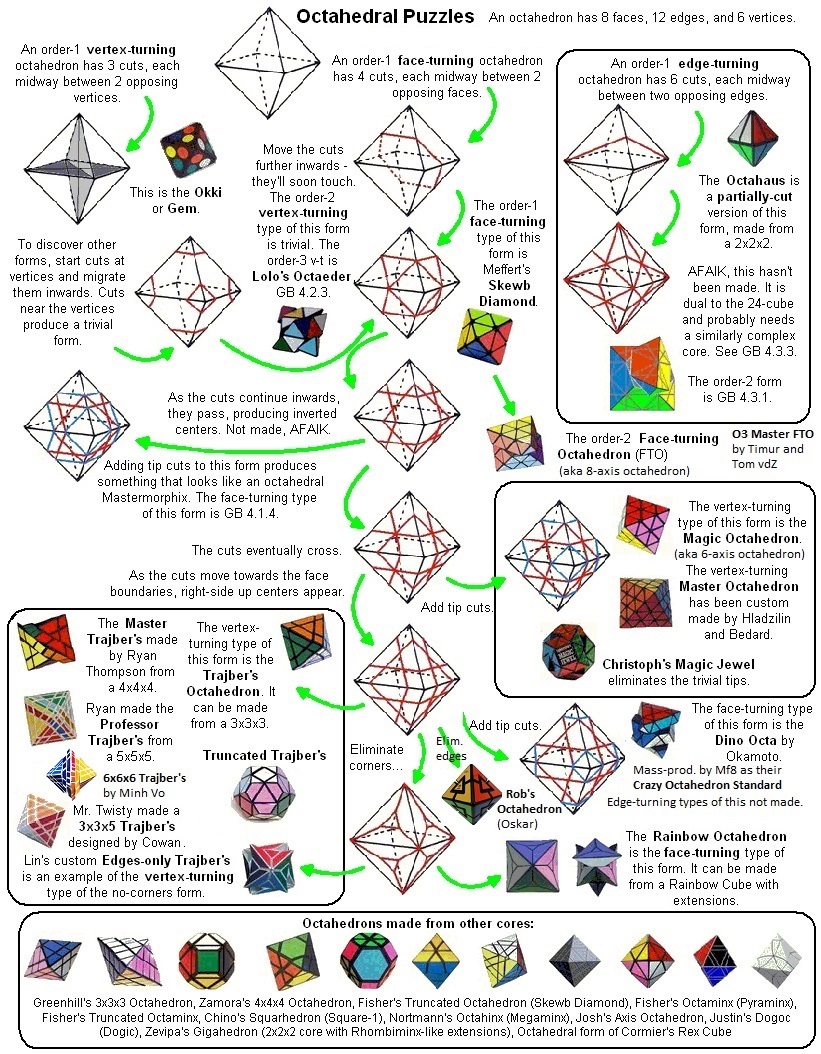
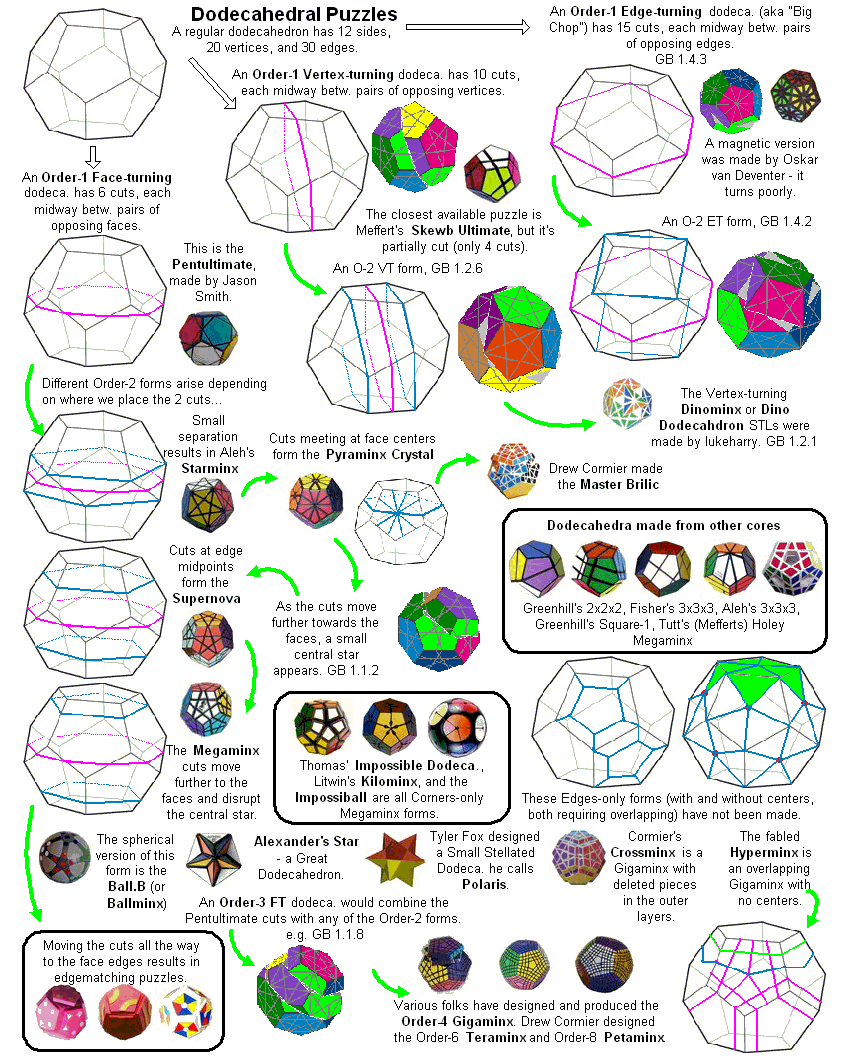
The illustration below shows many (not all!) of the twisty polyhedra (and some non-polyhedral) puzzles that are now or have in the past been mass-produced and commercially available.

Starting in 2010, a new wave of twisty puzzles hit the market, and many custom designs made it into mass production. More continue to arrive and it is impossible to keep up. Some puzzles are members of a series exploring variations on a theme - e.g. the "Planets" series of Crazy cubes and dodecahedrons, various bandaged cubes, and the "Bermuda" cubes - I have not attempted to show all the series members. Also, there are many different brands and types of the conventional face-turning cubes, including speed cubes, which often turn better than the Rubik's brand version. Usually the mechanical differences are not apparent in photos. I have also not attempted to show the many shape extensions of the FT cubes, including the "Crystal" shapes, nor all the 2x2x2 heads and objects.

Newcomers to twisty collecting have asked for a short list of essential puzzles, and many TP forum members have provided guidance. In the illustration below, I have identified 10 fundamental puzzles most collectors feel every twisty collection should contain. Based on collating various folks' recommendations, I have also identified a further 33 puzzles to extend a good collection. Of course, you eventually have to have them all, right?

Vertex/
Face
Turning
Tetrahedra
Royal Pyraminx
Edge
Turning
Tetrahedra
Ultramorphix - Shengshou (5-Layer Mastermorphix)
Other
Tetrahedra
Face
Turning
Cubes &
Cuboids
Vertex
Turning
Cubes
Honey Copter
Skewb
Vars.
Dino
Vars.
Edge
Turning
Cubes
Hybrid
Turning
Cubes
Flower Copter Skewby Copter Plus - Mf8 Morpho Aureola - FangShi Limcube Twins Cube - Mf8
Square 1
Family
Axised
Cubes
Crazy/
Circle/
Super
Cubes
Other
Cubes
Shape &
Sticker
Mods
2x2x2
Vars.
Face
Turning
Octahedra
Vertex
Turning
Octahedra
Edge
Turning
Octahedra
Other
Octahedra
Clover Octahedron - Verypuzzle Clover Octahedron Fragmentation
Face
Turning
Dodeca.
Vertex
Turning
Dodeca.
Edge
Turning
Dodeca.
Other
Dodeca.
Rhombic
Dodeca.
Icosahedra
DaYan
Gem
Series
Globall
Series
Verypuzzle
Series
Other
Shapes
Dihedral
Spheres
Edge-
matching

This section contains several definitions. You can click the "_" symbol to hide it, if you'd like.

Definitions:

  1. The basic form of a "twisty polyhedron puzzle" is a polyhedron (MathWorld, Wikipedia), although rounded shapes are traditionally included in the class, for example spheres, and cylinders or pucks (or "UFO"s).

  2. Polyhedra have been studied extensively since antiquity and formally classified, based on their features, and whether they are convex or concave (non-convex). For a comprehesive list, see George Hart's Encyclopedia of Polyhedra, or the Wikipedia page for Polyhedron. Only a few shapes have been used again and again as the basis for twisty polyhedra puzzles. Some have only appeared in custom puzzles. Polyhedra that are too spiky, too rounded, or too irregular might be of interest to a collector but probably won't make popular puzzles as they are difficult to handle and/or too difficult to visualize when solving.

    • The five Platonic Solids (regular convex polyhedra) - tetrahedron, cube, octahedron, dodecahedron, and icosahedron - have proven to be the most popular shapes, though the icosahedron is infrequently used.

    • There are four Kepler-Poinsot (regular non-convex) polyhedra - These shapes are also the result of stellation of some Platonic Solids. The tetrahderon and cube have no stellations. The octahedron has one stellation, called a stella octangula - that shape has appeared in the Starburst and the Dino Star. The dodecahedron has three stellations: the small stellated dodecahedron, the great dodecahedron, and the great stellated dodecahedron. Only the great dodecahedron has been used in a commercial puzzle - the Alexander's Star. There are 59 stellations of the icosahedron, one of which is the great icosahedron.

    • Some of the Prisms and Anti-Prisms have been made. The larger category here is Prismatoid polyhedra, which also includes pyramids, cupolas, frustums, and wedges. There are also several varieties of Bi- or Di-pyramids.

    • Of the 13 Archimedean (semi-regular convex) polyhedra, the truncated tetrahedron, cuboctahedron, truncated cube, truncated octahedron, rhombicuboctahedron, and truncated icosahedron (soccer ball) have appeared.

    • The 13 Archimedean Duals, or Catalan Solids have not been much used, except for the rhombic dodecahedron and rhombic triacontahedron. There are three stellations of the rhombic dodecahedron, the first, second, and third. These shapes have been used more for interlocking puzzles than twisty puzzles.

    • The 92 Johnson Solids have not been used much at all.

  3. A polyhedron becomes a twisty puzzle when it is cut into distinct pieces, and an internal mechanism preserves the coherence of all pieces while allowing groups of one or more pieces to be moved (a twist). After a move or twist, pieces have exchanged positions with other pieces and potentially changed their orientation. The objective of the puzzle is to mix up the pieces, then restore them to a specific target configuration.

  4. There are a variety of cutting schemes and internal mechanisms ("cores") that have been developed. You can see many of the relevant patents at Joshua Bell's website. Most mods are based on commercially available puzzle cores, though with the broader availability of improved design tools such as CAD and 3D printing, new and more complex mechanisms are easier to realize (such as those used in the Pentultimate and the 24 Cube).

    It may be better to classify puzzles by their use of internal mechanism, but I'm not sure I like that method. I think it's more interesting to challenge designers by specifying a shape, slicing format, turning mechanics, and other features, then let them figure out the necessary internals. Of course, this does make it hard to chart the various mods made from non-standard mechanisms such as the Square-1, or adaptations of the mechanism for one shape to make a different shape, resulting in weird asymmetric cuttings (Tony Fisher's Hexaminx - a cubic Megaminx - comes to mind). Chris Lohe has a nice, though not exhaustive, chart at his website, organized by mechanism versus shape.

    Here are several mechanisms and/or cutting formats:

    • Cuboids
      • AxAxA - A=2,3,4,5,6,7
      • AxBxB - 1x2x2 (Morph), 1x3x3 (Okamoto's Floppy Cube), 2x3x3 Domino, 3x2x2 Slim Tower and Franken Tower, 3x4x4 Specter and Chaos, 4x2x2 (Fisher 2003), 4x3x3 Phantom Cube, 5x3x3 Grown Tower and TF 2004, 5x4x4 TF 2003
      • AxBxC - 1x2x3, 2x3x4 Step Up Tower and TF 2003, 2x4x5 Chaos
      • These can be made in fully functional, extended, or "chaos" (multiple core + extended) forms.
    • The EastSheen A4 cube core allows interesting overlapping effects
    • Pyramorphix
    • Pyraminx/Skewb
    • Dino/Stella Octangula
    • Helicopter/Bevel
    • Hybrid
    • Chop (e.g. the 24 Cube)
    • Megaminx
    • Dogic

  5. Key features of a polyhedron include faces, vertices, and edges. Most twisty polyhedra puzzles will have different types of pieces corresponding to each of these features. A given face may have one or more center pieces, edge pieces (shared between faces), and corner pieces (again, shared between faces). Almost always, an edge joins two and only two faces, and the corner pieces (if present) are at vertices of the polyhedron. Faces and edges meet at a vertex, and define a particular vertex figure.

  1. Members of this puzzle category are distinguished from their Sliding Piece brethren in the Sequential Movement class in several ways. For twisty puzzles, pieces move in distinct groups. There is no frame and there are no levers or plungers. Also, the space of possible states is typically very large and it is unreasonable for a person to navigate directly from a mixed state toward a solved state (i.e. using "God's algorithm") - instead, a variety of operators or algorithms (i.e. specific sequences of particular twists) must be used in series, each of which accomplishes a subgoal leading towards better order by moving subsets of pieces in determined ways while leaving other subsets undisturbed. Expert solvers have memorized many useful operators, can quickly recognize patterns or states when a given operator will be useful, can keep track mentally of where they are in the midst of a sequence of moves, and can apply operators (sequences of twists) very rapidly with great manual dexterity. Sometimes operators learned for one puzzle can be useful on another type, but often a distinct set of operators must be learned for each different puzzle type.

  2. A Deep Cut puzzle's cuts divide it into halves. Otherwise, the puzzle is Shallow Cut, though there are gradations of shallowness, and some puzzles might have a few deep cuts mixed with shallow cuts. Alternatively, circumscribe a sphere around the puzzle, and project the cutting planes to intersect the sphere. If the projections make great circles on the sphere, the cut is deep. This disqualifies the Pyraminx ( Pyraminx setting on Jaap's Sphere) but includes the Skewb ( Skewb setting on Jaap's Sphere). Read a debate about the definition of "deep cut" in the TwistyPuzzles forums.

  3. If the cutting scheme results in sets of regular pieces, essentially interchangeable within their groups, then it is customary to distinguish them by coloring their individual faces. The overall pattern of colors will define the goal state of the puzzle. In other cases when the pieces are distinctly proportioned, the puzzle might be monochromatic and its goal state defined by shape alone.

  4. I've defined the order based on the number of parallel cuts (either deep or shallow) between opposite pairs of faces, vertices, or edges, or for tetrahedrons, opposing face-vertex pairs. Also note that the term slice is used ambiguously to mean either a cut itself, or a layer between two cuts or between a cut and the surface of the puzzle. My definition of order might be at odds with they way some people think about these puzzles - for example I define the 2x2x2 Pocket or Mini Cube as order 1 but some might define it as order 2 based on it having two "slices" in each dimension.

  5. Note that it is possible to construct puzzles with asymmetric slicing schemes - i.e. different numbers of parallel cuts between different pairs of opposite features. These would be characterized using compound orders.

  6. It is also possible to arrange the cuts so that they are either equally or unequally spaced between the features that bound them - the resulting slices are correspondingly either equal or unequal.

  7. Another irregularity results when not all opposite features have the same set of cuts between them, though those that do, have the same number of cuts between them - i.e. subsets of opposite features are treated differently. I call this a Partially Cut puzzle and distinguish it from a Fully Cut puzzle. This can be a consequence of creating a shape modification with a particular underlying core mechanism originally clothed in a different shape. An example is the dodecahedral Skewb Ultimate which has a Skewb core, originally clothed in a cube. The cube has eight vertices, and in the Skewb every pair of vertices has one (deep) cut between them, so four cuts suffice. The dodecahedron has 20 vertices or 10 pairs of opposing vertices. Since there are only four (deep) cuts, there is a cut between each of only four out of the ten pairs of opposing vertices.

  8. If all the pieces in a face move during a twist, the puzzle is Face-turning. If instead all the pieces around a vertex move, the puzzle is Vertex-turning. Similarly, if all the pieces along an edge move, the puzzle is Edge-turning. Hybrids are possible, but the internal mechanisms become complex, and the puzzle becomes very "squishy" since it is difficult to hold without inadvertently twisting something. In tetrahedra, the distinction between face and vertex turning is blurred, since a vertex is opposite a face.

  9. A sphere has no faces, vertices, or edges. A more useful distinction is how the cuts divide the surface, and how they intersect. The cuts can make great circles or small circles. By convention, two points at diametrically opposite locations on an arbitray great circle are chosen as poles. All great circles passing through the poles are longitudinal. One great circle can perpendicularly bisect all longitudes - this is the equator. Small circles parallel to the equator are latitudinal. Symmetrically arranged small circles are typically centered on regular polyhedra inscribed within the sphere.

  10. A cylinder or puck has two parallel circular faces with a curved surface between them. Cuts can be radial and divide the circular faces, or sectional and lie between the faces.

  11. So to classify the various species of twisty polyhedra puzzles by their physical characteristics, one could use the following criteria in some priority:
    • Shape
    • Order
    • Turning type - Face, Vertex, (Face/Vertex for tetrahedra), Edge, Hybrid
    • Cutting style - Deep vs. Shallow, Equal vs. Unequal, Full vs. Partial, Symmetric vs. Asymmetric; for spheres, layout of longitudinal, latitudinal, and small-circle cuts; for cylinders/pucks/ufos, layout of radial and sectional cuts
    • Features - Corners/Edges/Centers present?
    • Internal core mechanism
    • Decoration/coloring scheme

    One could additionally or alternatively use the total number of unique possible permutations or states, or some (subjective) rating of difficulty, or of rarity.

Notes on Variations and Mods

Notes About Sticker and Feature Variations

A standard face-turning 33 has 26 visible moving parts (usually referred to as "cubies")- 8 corners, 6 face centers, and 12 edges, plus an internal core - a six-armed "spider."

As faces are turned, the corners and the edges permute (i.e. exchange positions with each other) in separate groups. The six face centers of the basic 33 are attached to the ends of the internal spider, so are fixed relative to each other and do not permute. Each cubie can also assume different orientations depending on type:

We assume that neither corners nor edges can be re-oriented if they cannot first be permuted, since unlike the face centers they do not twist in place.

Each corner exposes three "facelets" - each face center one, and each edge two, for a grand total of 8x3+6x1+12x2= 54 facelets. A sticker pattern is applied to the facelets, and is used to either make apparent or hide the permutations and orientations of the cubies.

Each facelet is usually covered with one sticker. In the standard configuration there are nine stickers of each of six different colors, and each of the six faces of the cube is stickered with a solid color. The basic sticker pattern has varied with respect to the six colors used and how they are arranged relative to each other. In addition, one or more stickers might bear a logo of some sort.

As the cube is twisted, the color arrangement becomes scrambled. The objective of the puzzle is to unscramble a scrambled cube, restoring the canonical color pattern on all faces simultaneously.

Sticker variations can serve four basic purposes:
1) pure decoration
2) advertising promotion
3) modify the difficulty of the basic coloring, without changing the basic objective of restoring a canonical pattern
4) alter the goal of the puzzle (e.g. calendar cube, sudo-kube)

Personally, I am uninterested in sticker variations of the 1st or 2nd varieties, except insofar as they simultaneously accomplish the 3rd or 4th purpose.

So, for a 3x3x3 with a uniform pattern, we have the following possible fundamentally different sticker variations:

3x Faces: (permutations not possible) - NO orientations visible (N), ALL orientations visible (A), or 180s obscured (O)
3x Edges: neither permutations nor orientations visible (N), permutations only visible (P), or both permutations and orientations visible (P+O)
3x Corners: N, P, or P+O

This gives 27 possibilities:

F:N
  • E:N
    • C:N = an unstickered cube, eq. to a 1x1x1
    • C:P = eq. to the PyraDiamond - a 2x2x2 with truncated corners
    • C:P+O = eq. to the standard 2x2x2
  • E:P
    • C:N
    • C:P
    • C:P+O
  • E:P+O
    • C:N = the traditional or void "edges-only" cube
    • C:P = eq. to the truncated Trajber's Octahedron
    • C:P+O = the standard 3x3x3 pattern
F:A
  • E:N
    • C:N = the simple babyface
    • C:P = an 8-color simple overlapping cube
    • C:P+O = a 12-color simple overlapping cube
  • E:P
    • C:N
    • C:P
    • C:P+O = eq. to the 3x3x3 Rhombic Dodecahedron
  • E:P+O
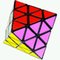
    • C:N = eq. to the Magic Octahedron or Christoph's Jewel
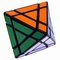
    • C:P = an 8-color cube; eq. to the Trajber's Octahedron
    • C:P+O = a "Super Cube" - commercially produced as the Ultimate Cube
F:O
  • E:N
    • C:N
    • C:P
    • C:P+O
  • E:P
    • C:N
    • C:P
    • C:P+O
  • E:P+O
    • C:N
    • C:P
    • C:P+O

Andreas Nortmann explores the first 18 members of this series in the TP forums.

We might also imagine applying the pattern non-uniformly - for example, making only a subset of the edge and corner permutations matter (and none of the orientations matter), as in the tri-color cube, or making only a subset of the face orientations matter, as in the Fisher Cube or the Rubik's Cube Fourth Dimension.


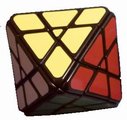
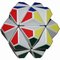
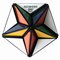
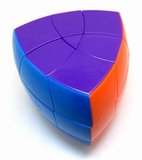
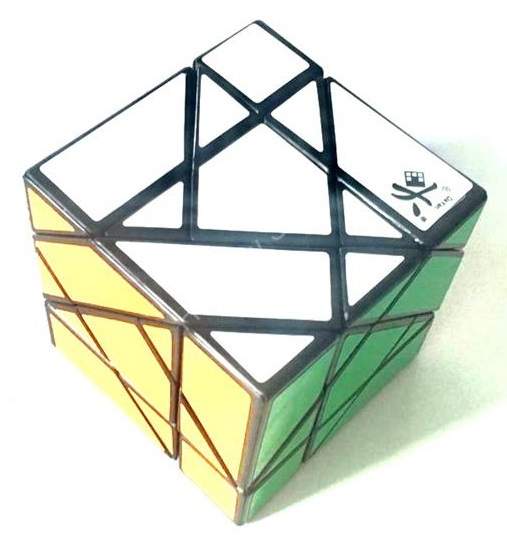
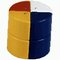
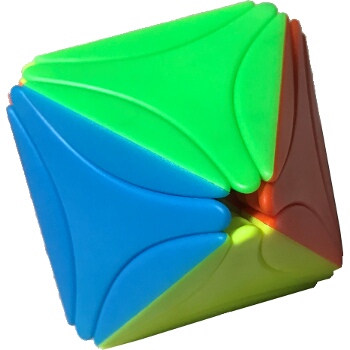
Tri-color Cube
Fisher's Cube
Fourth Dimension

Note that sticker variations are different from feature variations. Feature variations arise when actual physical features are present or absent. Any features that are present can, in turn, be stickered according to the possible variations. Also, feature variations can be used in lieu of sticker variations to enforce the visibility of some specific permutations or orientations.

A physical design might be contrived to disguise or eliminate face centers, corners, edges, or combinations thereof. This may necessitate allowing pieces to overlap as they turn past one another as the trajectory of the cut on the surface of the puzzle no longer follows the path of a great circle equivalent. Lately it has also become possible to eliminate the central core, forming a "Void" or "Holey" cube.

If we apply a uniform variation to all like features of a cube, we have the following possibilities:

  • FEC -  - all features present
  • FEN -  faces and edges but no corners - can be implemented in different ways:
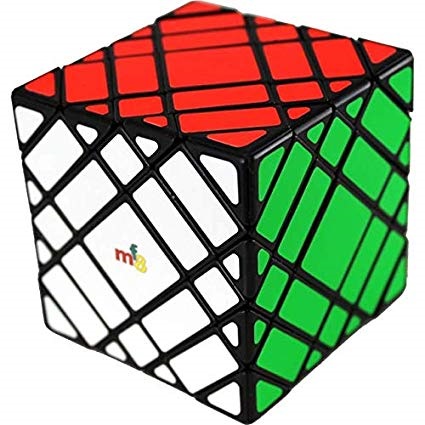
    • - this is what is typically referred to as an "edges-only" cube even though technically that's inaccurate (4x4x4 also shown)
    • - by simply shaving down and blacking out the corners
  • FNC -  faces and corners but no edges - can be implemented in different ways:
    • - as a "simple overlapping cube" (4x4x4 version also shown)
    • - by simply shaving down and blacking out the edges - the "Corners Cube"
    • - taking this to its extreme, we end up with Oskar van Deventer's "Gerardo's Cube"
  • FNN -  faces only - can be implemented in different ways:
    • - a "babyface" cube - each face can be turned (oriented) in place, colored to make an edgematching challenge (4x4x4 Babyface also shown)
    • - Oskar van Deventer has created the PantaCube, which has only five of six faces but allows those five faces to be permuted.
  • NEC -  edges and corners but no faces - can be implemented in different ways:
    • Eliminate the core, as in the Void or Holey Cube
    • Hide the faces using overlapping, as in the "Brilicube"
    • Just sticker all six faces gray or leave them unstickered - i.e. ignore them - which isn't really a feature variation after all, more a sticker variation
  • NEN -  true edges-only - can be implemented in different ways:
    • Using a Void Cube, cutting down and hiding the corners, then extending the edges to overlap them - this has been mass-produced.
    • Extending edge plates to overlap hidden face centers and corners, so the cuts make a big X on each side (4x4x4 version also shown)
  • NNC -  - true corners-only - since any size cube has only eight corner pieces, this boils down to the basic 2x2x2
    Also consider the Nightmare Cube, in which overlapping corner pieces hide an internal 3x3x3 that has been bandaged.
  • NNN - nothing moves - this is the trivial 1x1x1

Andreas Nortmann discusses these variants in the TP forums.

Edges and corners can also be truncated rather than entirely eliminated. Furthermore, we might elect to apply feature variations selectively to only a subset of cubies. Andreas Nortmann has created the series of all possible corner truncations of the 3x3x3 and shows it in the TP forums. (And earlier, here.)

Sticker and/or feature variations will differentiate one puzzle from another otherwise of the same order, and can dictate different solution methods. In the most complex case, you need algorithms to permute corners, orient corners, permute edges, orient edges, and orient faces. (The PantaCube, and the Cubedron family, require algorithms to permute faces.)

Lastly, all we've said here about sticker and feature variations regarding the face-turning 3x3x3 cube, could be applied sytematically to other orders, to other turning regimes, and to other shapes.

Notes About Twisty Mods

To "mod" or modify a twisty puzzle is to create a customized version of a puzzle, usually by starting with one of the commercially available puzzles and making various modifications, or sometimes by building a new variety from scratch.

New custom puzzles will continue to be made and there will always be some new design-of-the-hour not covered here. To keep abreast of the latest developments, you should monitor the Twisty Puzzles forums.

Some designs will make it into production while others will be forgotten or remembered only as impractical curiosities. Artists will come and go, and pass away.

There are several people who have become fairly well-known in the twisty puzzle community for their custom creations, and many creations which have become recognized as "classics." Here are just a few:

  • Tyler Fox - ceated the Gigaminx.
  • Adam Cowan - Axis Cube, Helicopter Cube
  • Jason Smith - Pentultimate - see Jason's website Puzzleforge.com for a detailed look into the genesis of this puzzle. Read more about its history on TwistyPuzzles.com in this thread.
  • Drew Cormier - Master (Halpern-Meier) Tetrahedron, Master Skewb, Teraminx, Petaminx - see Drew's YouTube channel
  • Matt Shepit - Cheeseblock, Toru, Rua (face-turning RD), Danger Cube (pillowed tetrahedral Square-1), The 24 Cube thread and video - see Matt's YouTube channel
  • "Pink"

There has been a flowering of new designs, brought on by broader knowledge of and availability of CAD design tools that can output STL, and 3-D Printing services (e.g. Shapeways, 3dpartz.com, printo3d.com ) that can take STL input and make master parts or full prints.

Here are some CAD tools:

There is also greater awareness of materials and techniques for casting parts from polyurethane plastic resin (e.g. Conap, Alumilite - get some at Hobby Engineering) using silicone rubber (e.g. Oomoo 25 or 30 - longer pot life, but longer cure time) two part molds poured in a Lego box. Don't forget a mold release agent such as Mann Ease Release 800 or 200. See the articles at TwistyPuzzles. Also this thread.

The traditional methods include cut-downs using a Dremel or hacksaw, and build-ups using Apoxie Sculpt (also here), Milliput, 1/8" ABS plastic sheet, or .040" polystyrene sheet. You can find materials at McMaster.

Many mods will use a black DIY core.

Use a Stika or some other vinyl sheet cutter (e.g. US Cutter) to create the stickers from Oracal 651 vinyl adhesive sheet.

This section contains a series of charts I made to organize my thinking about the relationships among various puzzles of each shape. You can click the "_" symbol to hide it, if you'd like.

The illustration below is my attempt to provide a fun "map" of the Twisty Polyhedra puzzle landscape, including most of the commercially produced puzzles as well as several of the interesting hand-made custom modifications. I have exercised personal judgement as to what to include or exclude, and though I have tried to be comprehensive there is no way I could be complete. Photos are from several sources, including Sandy's TwistyPuzzles.com, Jaap's Puzzle Page, and Hendrik Haak's PuzzleMuseum.

The basis of the map is a central pentagon, having the five regular Platonic solids at its vertices (the yellow circles). At the center of each vertex circle is the key commercially produced puzzle having that shape. Those and other key commercially produced puzzles are outlined in red. Spherical puzzles radiate outward from the center of the pentagon. For the most part, derivatives of the key puzzles are shown near their relations, though some placements may be problematic. Some interesting cube sticker variations and bandaged cubes are shown in the upper left, and cube derivatives in the upper right. The families of derivatives of the Skewb and the Square-1 are shown in bubbles on the left. A group of rhombic octahedra appear on the right, and a group of dihedral puzzles in the lower right. Radiating "arms" show the different sizes of Rubik's Cube, and puzzles related to the Dino Cube.

Here is a new chart updated as of Feb. 2020:

Catalogue of Twisty Polyhedra

The following sections catalogue polyhedral twisty puzzles in my collection.

A while back I snagged a Usenet post of a list compiled by Mark Longridge (March 22, 1996) in which rearrangement puzzles were ranked by number of combinations. That list gave me the idea for the organization scheme I originally employed here. However, I have revised the catalogue to better group related puzzles.

I include a few puzzles I do not own, for reference - they are noted as such by using this particular background color for their row.

Custom-made or 3D printed puzzles are highlighted like this.

For the best catalogue of twisty puzzles, I don't think one can beat the museum section at TwistyPuzzles.com. The curators and Andreas Nortmann in particular have done a fantastic job!

Jaap's Puzzle Page was also invaluable in teaching me what puzzles were out there, and for providing combinations data for several puzzles.

The number of permutations, positions, or states a puzzle can achieve is not always a good indicator of difficulty. Many cubers rank the Square-1 as more difficult to solve than many puzzles with larger numbers of permutations. I have not attempted to rank the puzzles by difficulty.

My favorites include the Pyraminx (I worked out solution procedures myself), the Square 1 (I wrote a program to explore moves), the Impossiball (I've had it for a long time though I've never solved it, and I love its organic motion), and the Skewb (its motion is so precise). I also like the Orb[-it]. I got a Masterball in Japan and the Tonne in Germany.

Tetrahedral Twisties

F/VE
O1O2O3+O1O2O3+















 

 

 






 


 

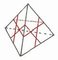
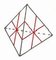
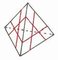
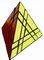
Face/Vertex-turning Order 1
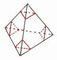
 ==>  Move cuts from tips inwards until they touch, forming inverted triangles on faces...
Space Pyramid
Space Pyramid
Just trivial tips.
"Junior Pyraminx" [T]; "Mini Pyraminx" [T]
Hoberman Brain Twist

 Hoberman Brain Twist

From a company not known for twisty puzzles. A unique take on what would otherwise be a trivial vertex-turning tetrahedron - the tips invert and you can turn the whole puzzle kind of "inside-out." This idea has not been used on any other twisty AFAIK.

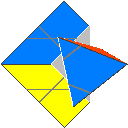
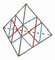
Continue moving the cuts from the vertices towards the opposite faces -
three different basic forms result...
(All can have tip cuts, which result in either trivial tips on vertex-turning forms,
or edge-turning O2 forms.)


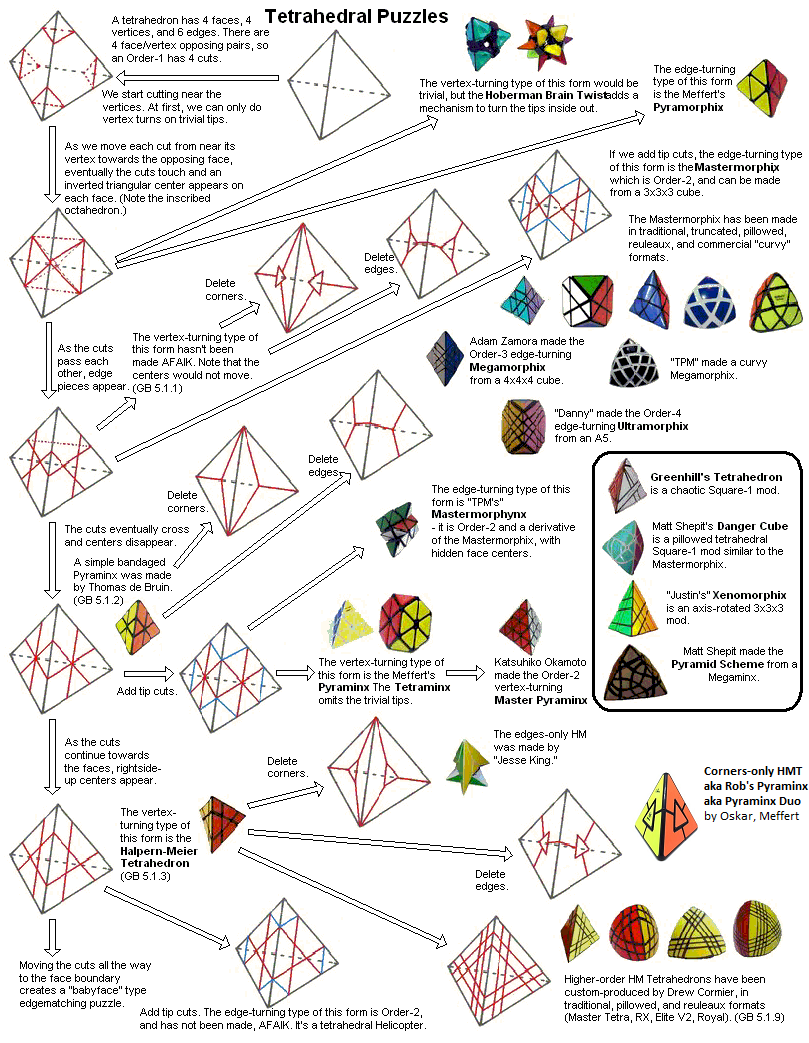
GB 5.1.1 - Pyramiddle - Justin

 The first of these is GB 5.1.1. It has stationary centers. TP member Justin built one and calls it Pyramiddle. [T]
Pyraminx - GB 5.1.2 - Meffert
9.3*105 = 933,120 (not including trivial tips);
7.6*107 = 75,582,720 (with tips)
- Uwe Meffert - 4-armed spider

The Pyraminx
An original issued by Tomy, loose and in package, a Meffert's 25th Anniversary version, and Meffert's New Pyraminx, in black.
Also a QiYi stickerless Pyraminx.

The Pyraminx is not deep-cut.

Solving the Pyraminx
  1. Align the trivial tips so their face colors match the base pieces to which they are attached.
  2. Rotate the base+tips until all four faces each have 3 base+tips of a single color.
  3. Ensuring the base+tips remain solved, move edge pieces around intuitively until you either end up solved, or with two edges left which are in place but flipped (e.g. A and B), or a case where three edges need to be cycled around a tip (e.g. A, B, and C).
  4. Use either of the algorithms shown here to finish.

My operator to flip two edges A and B in place:

L T' R T
R' T L' T'

When 3 edges around the top would be solved if only you could circulate them clockwise (i.e. A->C->B->A):

(R T' R') T' (R T' R')

To instead cycle them counterclockwise, change all T bars to T.

Also see the HMT/Jing's Pyraminx for a design requiring face center permutations.

Also check out the Petal Pyramid.

Special Edition Pyraminx designed by Sam Baron for the Louvre

Ligne Pyramide Pei Ligne Pyramide Pei Ligne Pyramide Pei

Ligne Pyramide Pei -
This special edition Pyraminx designed by Sam Baron for the Louvre
is decorated to evoke the famous and controversial glass Pyramid
installed in the courtyard of the Louvre by the architect I. M. Pei.
Purchased in the Louvre gift shop.
Here is the view from inside the Pei Pyramide looking out...

Inside Pyramide Pei

Pyraminx Deluxe

Pyraminx Deluxe Pyraminx Deluxe

Pyraminx Deluxe Limited Edition - issued by Recent Toys
This version has wood-grain tiles.
Pyraminx 50th Anniversary Crystal Edition

 50th Anniversary Crystal Pyraminx
Bandaged Pyraminx

 The tetrahedral version without trivial tip cuts is the Bandaged Pyraminx, built by Thomas de Bruin [T]
I don't have this.
Tetraminx (Pyraminx sans trivial tips)

 Tetraminx
(A Snub Pyraminx - same as Pyraminx with trivial tips removed.)
Mefferts version, and transparent version from Smaz.
Round Pyraminx / Penrose Pyraminx - Mason Hynds - Yuxin

 Round Pyraminx / Penrose Pyraminx - Mason Hynds - Yuxin
Some states look like parity, but remember the small rounded edge pieces are symmetric. Solves like the Pyraminx.
Cubominx (Tony Fisher)/ Eye-Skewb (Eitan Cher)

 A Pyraminx/Tetraminx (or Skewb) can be modded to a Cubominx [T] [T] [T] [Y] which is kind of a "half-Skewb" - curvy cuts give Eitan's Eye-Skewb [T]

Ivy Cube

 Eitan's Eye-Skewb [T] has been mass-produced by QiYi and released as the Ivy Cube
It is a variation of the Cubominx designed by Tony Fisher [Y] which was based on a Pyraminx.
Solving the Ivy Cube
The Ivy Cube has an eye-shaped petal on each face. There are four corners where three eye tips meet at the corner (see 1st diagram), and the other four corners each of which is instead surrounded by three eyes but has no eye tip touching it (see 2nd diagram).
  1. Turn corners until the two non-eye pieces on each face are the same color..
  2. Use the two algorithms given here to solve the eyes/petals.

In the first diagram (where three eye tips meet), cycle A->B->C->A ccw using:

R L' R' L

or clockwise using:

L' R L R'

In the second diagram (no tips touch), cycle A->B->C->A ccw using:

R F R' F R F R'

To instead cycle them clockwise, change all F to F'.

Setup moves may be useful.

Six Spot Cube - David Pitcher - QiYi

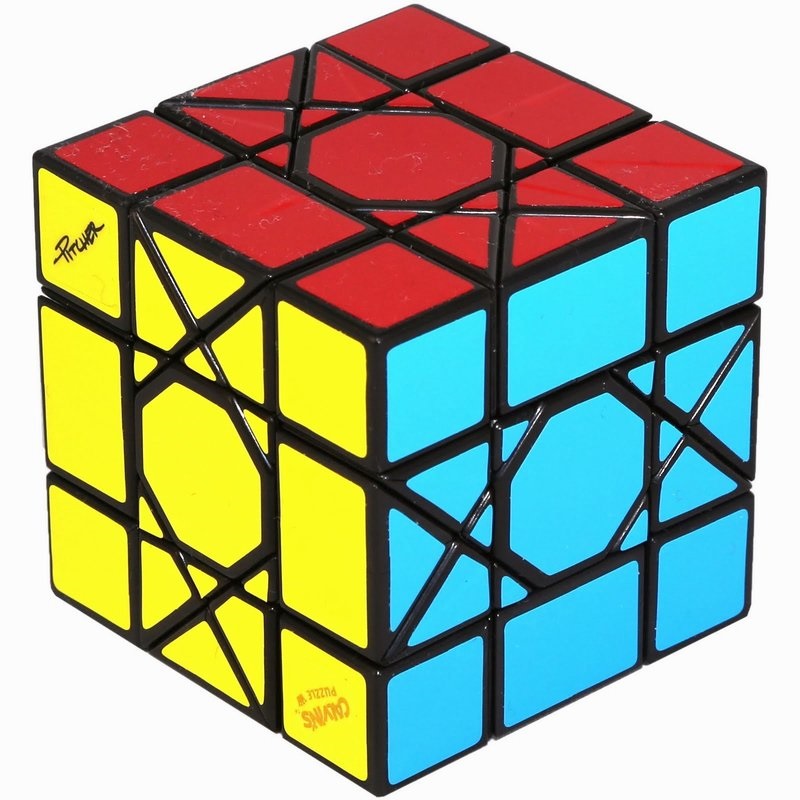
Six Spot Cube - David Pitcher - QiYi

Six Spot Cube - designed by David Pitcher, produced by QiYi
A variant of the Ivy Cube with circles rather than petals/eyes.
Yeet Ball - YongJun

 YongJun Yeet Ball (this is a spherical version of the Ivy Cube / Eye Skewb)
Unicorn Cube - Moyu

 Unicorn Cube - Moyu
This is a trivial "puzzle" - essentially a face-center-less (eyeless?) version of the Ivy Cube. The same set of only four corners that can turn, but no face centers to permute. To solve, just align the turning corners to render each face monochromatic.
Jewel Tetrahedron - Grigorusha (Edges-only Pyraminx)

 Jewel Tetrahedron - Grigorusha (Edges-only Pyraminx)
This can get to a state with only a single edge flipped.

Halpern-Meier Tetrahedron - GB 5.1.3 - Matt Davis
3.7*106 3,732,480 - Ben Halpern, Kersten Meier

This version of the order-1 tetrahedron is called Halpern's Tetrahedron or the Halpern-Meier Tetrahedron.
The HMT is deep-cut - all cuts go through its center.

This was produced commercially but that vintage version is very rare. I have a custom-built example made by Matt Davis from cast pieces and a Skewb keychain core. Also shown is a comparison with a Skewb.

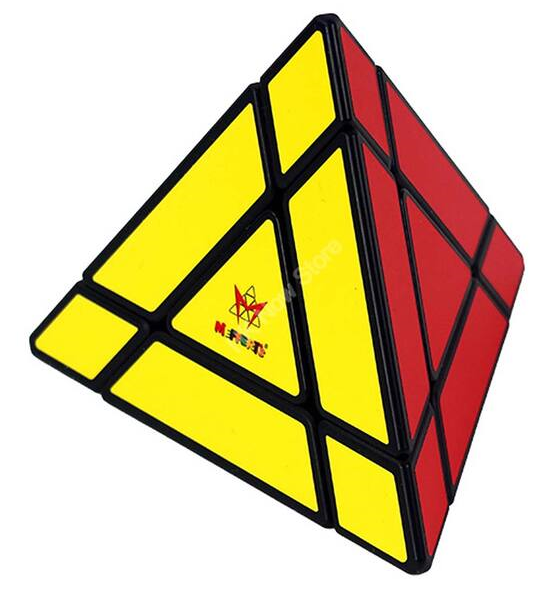
Halpern-Meier Tetrahedron (HMT) / Flat Jing's Pyraminx - Meffert

Meffert's Flat Jing's Pyraminx (HMT)
Jing's Pyraminx - GB 5.1.3 - Meffert

Meffert produced a Reuleaux version of the HMT, designed by Adam Cowan. They call it Jing's Pyraminx. It is fairly large. Also shown is the Jade Club Pyraminx, which is smaller than the custom HMT.

Solving the HMT / Jing's Pyraminx
The Halpern-Meier Tetrahedron / Jing's Pyraminx solves like the Pyraminx, but also has face centers which may have to be permuted at the end.
  1. Rotate the tips until all four faces each have 3 tips of a single color.
  2. Ensuring the tips remain solved, move edge pieces around intuitively until you either end up solved, or with two edges left which are in place but flipped (e.g. A and B), or a case where three edges need to be cycled around a tip (e.g. A, B, and C).
  3. Use the Pyraminx edge algorithms to solve the edges.
  4. Solve the face centers using the algorithms shown here.

In the diagram l, r, f, and d represent the left, right, front, and down face centers.
Swap pairs f<->l and r<->d using:

(T' R' T R)*3

This face center algorithm is also useful for solving the Pyraminx Duo.

Halpern-Meier Tetrahedron (HMT) - Shengshou

 Pillowed Halpern-Meier Tetrahedron (HMT) - Shengshou
aka 7-Segment Pyraminx
If you missed out on Jing's Pyraminx from Meffert, now you may be able to find a pillowed HMT from Shengshou.
Duomo Cube - Halpern-Meier Tetrahedron (HMT) - Justin Eplett / QiYi

 Duomo Cube - a visually striking, but functionally identical version of the Halpern-Meier Tetrahedron (HMT) - designed back in 2014 by Justin Eplett [T] [T], mass-produced by QiYi
Edgeless HMT - Rob's Pyraminx - Pyraminx Duo

 I am honored that the multi-talented Dutch puzzlist Oskar van Deventer [W] [S] has named one of his puzzle designs after me - Rob's Pyraminx. [T] Oskar named this previously unrealized (AFAIK) design after noticing it in my "family tree" chart of tetrahedral twisty puzzles.

Meffert's has mass-produced Rob's Pyraminx - for commercial release it is called the Pyraminx Duo.

The Pyraminx Duo is arguably the simplest non-trivial twisty puzzle - it is easy to solve intuitively and makes a fun gift for folks who normally wouldn't consider themselves avid puzzlers. If you would never even think of attempting a Rubik's Cube, don't worry - you can solve this! With its intriguing geometric shape, it looks great, too, and would be equally at home on an executive's desk or a teen's bookshelf.

Oscar Roth Andersen has even devised a game that can be played with the Pyraminx Duo!

Solving the Edgeless HMT / Rob's Pyraminx / Pyraminx Duo
The Pyraminx Duo is always a maxiumum of four moves away from solved! For a given state, you can discover the necessary four moves by careful inspection. However, you can also solve following the steps here, probably requiring more than four moves...
  1. Rotate the tips until all four faces each have 3 tips of a single color.
  2. Solve the face centers using a simplified variant of the HMT face center algorithms, shown here.

In the diagram l, r, f, and d represent the left, right, front, and down face centers.
Swap pairs f<->l and r<->d using:

T' R' T R

Unlike as with the HMT, you needn't thrice repeat the basic sequence - there are no edges to fix.

Another handy and similar algorithm swaps l<->r and f<->d:

R' L R L'

This latter algorithm can be executed quickly when you hold the puzzle using your right hand on R and your left hand on L.

Cornerless HMT

 The HMT has been made in cornerless form, by "jesseking." Also by "kwsjack054" [T]

See the MoYu Windmill Pyramid below for a mass-produced version.

Cornerless HMT / Ivy Mastermorphix - QiYi

QiYi Ivy Mastermorphix - this puzzle is isomorphic to a cornerless (edges-only with face centers) HMT.
Vertex turns are equivalent to opposite face turns but in this puzzle it feels more natural to turn a face rather than a vertex.

Magical Pyramid Puzzle Series - MoYu

Magical Pyramid Puzzle Series - MoYu
MoYu produced this set of six variations on the vertex/face-turning tetrahedron. I have arranged them in this 2-row by 3-column grid to show the relationships.

The first row contains variations on the Pyraminx - the puzzle in the first column, which MoYu calls the "Maple Leaf Pyramid" is like the Pyraminx without the trivial tips - there are corner pieces and edge pieces - but as in the Pyraminx, this entire row lacks centers. Note that the Maple Leaf Pyramid resembles the edge-turning Clover Pyraminx mass-produced by QiYi, though it lacks that puzzle's small face centers.

The second row contains variations on the HMT - the puzzle in the first column, which MoYu calls the "Triangle Pyramid" - is equal to the HMT, having (right-side-up) centers, corners, and edges, all of which move as expected.

The second column contains the respective edgeless variants, and the third column contains the respective cornerless variants.

The "Corner-twist Pyramid" had been shown in my family chart of tetrahedral puzzles but AFAIK had never been produced (it is trivial to solve). The "Boomerang Pyramid" is equivalent to Grigorusha's custom Jewel Tetrahedron.

The "Bead Pyramid" is equivalent to Oskar's "Rob's Pyraminx" / Pyraminx Duo. The "Windmill Pyramid" is equivalent to the custom Cornerless HMT shown above, and I am happy to finally have this mass-produced version.

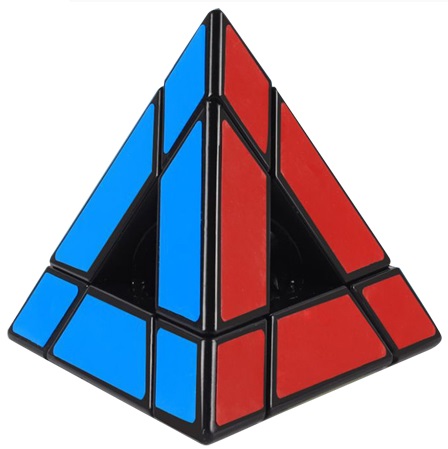
Void HMT

Sengso Void Pyramid (Void HMT)
A high quality puzzle - I really like this one. Since the face centers are missing, it solves like the Pyraminx.
Bump/Mirror HMT

Sengso Mirror Pyramid (Bump HMT)
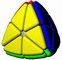
24 Tetrahedron (magnetic) - Tanner Frisby

 24 Tetrahedron
6 Cuts - every edge is bisected - each cut is a plane that goes through the midpoint of an edge and coincides with the opposite edge. A turn moves half the puzzle.
Magnetic version by Tanner Frisby [T]

Claus Wernicke built one based on the 24 Cube by Matt Shepit. [T]

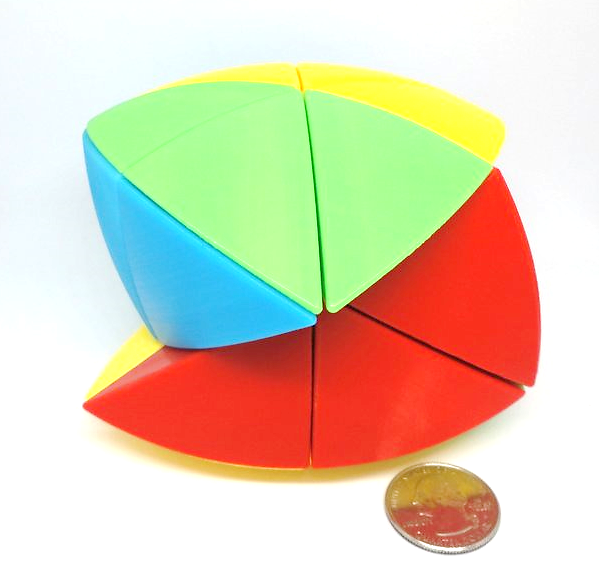
24 Tetrahedron (Chromium mech.) - James Li

 24 Tetrahedron (Chromium mech.) - James Li
6 Cuts - every edge is bisected - each cut is a plane that goes through the midpoint of an edge and coincides with the opposite edge. A turn moves half the puzzle.

Shown with the Sengso Master HMT.

Face/Vertex-turning Order 2
Master Pyraminx - GB 5.1.4 - Evbatyrov / Cowan / Meffert
2.2*1014 positions ignoring trivial tips.

The Master Pyraminx, issued by Mefferts
Designed by Timur Evbatyrov and Adam Cowan
Another great design mass produced beautifully by Meffert!

For the longest time, Meffert could not find a way to produce the next higher order relations to his Pyraminx. Early custom puzzles made by Japanese modder Katsuhiko Okamoto [T], while clever and beautiful, were considered too fragile for the mass market. Back in late 2008 Cowan pioneered the use of the reuleaux tetrahedron to solve some of the design issues: wikipedia, [T], and Timur Evbatyrov was the first to offer a reasonably priced master pyraminx via his shapeways shop.

Shim's Master Pyraminx - Timur Evbatyrov

 I dyed, assembled, and stickered my Shim's Master Pyraminx. I really like this puzzle! It was designed by Timur Evbatyrov and is available on Shapeways.

Two photos show relative size - a comparison with an original Tomy Pyraminx, and a group photo including various tetrahedral twisty puzzles.

The group photo includes, left to right, row by row from the top: the Hoberman BrainTwist, Meffert's Jing's Pyraminx (designed by Adam Cowan), Meffert's NGP (Platypus), Tomy Pyraminx, a custom Halpern-Meier Tetrahedron (keychain Skewb core) made by Matt Davis, Meffert's Pyramorphinx (a curvy Mastermorphix), Traiphum Prungtaengkit's (Traiphumi's) Mastermorphynx (a custom-made edge-turning Pyraminx), a keychain Meffert's Pyramorphi[n]x, Shim's Master Pyraminx, and a reuleaux Babymorphix custom-made by Taylor Howell.

Shengshou 4-layer / Master Pyraminx - GB 5.1.4

 Master Pyraminx from Shengshou
QiYi 4-layer / Master Pyraminx - GB 5.1.4

 Master Pyraminx from QiYi - stickerless version
Confusion Pyramid / Hyper HMT (Fourth Magic Tower) - Sengso

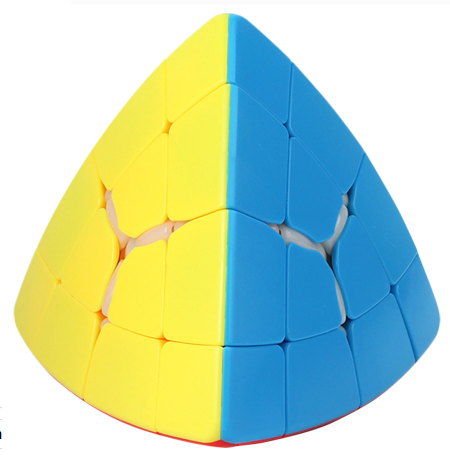
 A pillowed order-2 HMT that slots in before the true Master Tetrahedron / RX, has been mass-produced by Sengso / Shengshou - they call it the "Fourth Magic Tower." I think of it as a "Hyper HMT."
It deletes face centers and the inner and outer edges that abut them, very similar in principle to how the Hyperminx (commercially sold as the Master Kilominx and slotting in before the Gigaminx) also deletes centers and two layers of abutting edges.
Mentioned by TP member Cow7 in 2010 [T].
Realized by TP member Muffet, who called it "Confusion Pyramid" in 2012 [T]. Mass-produced by Sengso in 2021.
Master Tetrahedron / Master HMT

 The order-2 HMT is called a Master Tetrahedron. First made by Drew Cormier [T] [T].
Drew also made a pillowed version he called the RX.

I obtained a Reuleaux Master Tetrahedron made by Hung Nguyen (cublem).

Master Tetrahedron / Master HMT

 A pillowed order-2 HMT / Master Tetrahedron / RX has been mass-produced by Sengso / Shengshou - they call it the "Fifth Magic Tower."
Face/Vertex-turning Order 3+
Professor Pyraminx - GB 5.1.10 - Timur Evbatyrov / Meffert

 The Professor Pyraminx, issued by Mefferts
Designed by Timur Evbatyrov
Yet another great design from Timur, mass produced beautifully by Meffert! I love this puzzle!
Elite Hyper HMT (Sixth Magic Tower) - Sengso

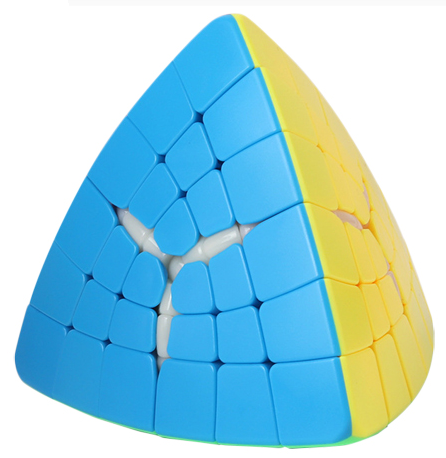
 This order-3 variation of the HMT relates to the order-3 Elite HMT below in the same way that the order-2 "Hyper HMT" (Fourth Magic Tower) relates to the order-2 Master HMT.
It deletes face centers and the inner and outer edges that abut them. This has been mass-produced by Sengso / Shengshou - they call it the "Sixth Magic Tower." I think of it as an "Elite Hyper HMT."
Elite Tetrahedron / Elite HMT - Chris Hemerich

 Elite Tetrahedron

The Elite Tetrahedron was first made by Drew Cormier [T] [T] [T]

This pillowed version was made for me by Chris Hemerich [T] [T] [S] [Y]

The Elite Tetrahedron is also shown in comparison to Meffert's Professor Pyraminx and Vergo's Master Pentultimate.

Elite Tetrahedron / Elite HMT (Seventh Magic Tower) - Sengso

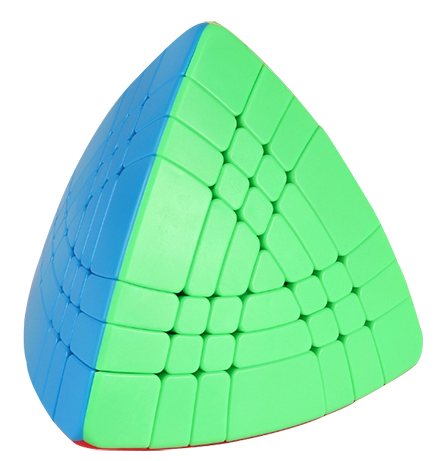
 A mass-produced order-3 HMT from Sengso / Shengshou
Order-4 Pyraminx / Royal Pyraminx - Timur Evbatyrov

Royal Pyraminx

The Royal Pyraminx
Designed by Timur Evbatyrov
Originally custom 3D-printed, now mass-produced by Calvin's Puzzle
I got a blue collector's edition.
Order-4 HMT / Royal Tetrahedron - Drew Cormier

 The order-4 HMT is Drew's Royal Tetrahedron. [T]
Order-5 Pyraminx / Emperor Pyraminx - Timur Evbatyrov

Royal Pyraminx

Timur's order-5 Pyraminx.
Available for $320 at Evgeniy Grigoriev's Etsy shop.
Also at Timur's Shapeways shop.
[T]
Order-6 HMT - Gregoire Pfennig

Royal Pyraminx

Greg's order-6 HMT. [T]
Edge-turning Order 1
Pyramorphix / Pyramorphinx / Ruby's Triangle / Figurenmatch
136,080 - Rubik, Barry Lockwood

Pyramorphix aka Pyramorphinx, with various clones
Also the East German FigurenMatch
Jaap's page

This can be solved in the same way as a 2x2x2.

Babymorphix - Taylor Howell

 The Babymorphix is a Reuleaux Pyramorphix, custom-made by Taylor Howell.
Shengshou 2x2 Mastermorphix (Babymorphix)

 A mass-produced Shengshou 2x2 Mastermorphix (Babymorphix).
Edge-turning Order 2
Mastermorphix - GB 5.2.3


 Mastermorphix

This is a 3x3x3 mod. Center orientations matter. Back in 2005, these were not mass-produced, and hand-made custom versions could sell for over $100.

Traditional version designed by Tony Fisher, produced in China, offered with official Fisher stickers by Meffert's - black and white versions. Meffert's "Master Pyramorphinx" (the "curvy" version). Also known as a "Rice Dumpling" (stickerless).

Reuleaux Leaf Tetrahedron - Cornerless Mastermorphix - Uhrik

 Reuleaux Leaf Tetrahedron - designed and 3D printed by Kevin and Jenna Uhrik
See their Etsy shop The Puzzle Artists.
This is effectively a cornerless Mastermorphix, but the curved cuts allow jumbling-like moves.
NOTE that Qiyi offers a mass-produced non-curved version they call the Clover Pyraminx for about $12.
Clover Pyraminx - QiYi

 Clover Pyraminx - QiYi
Edge-turning Order 2
Mastermorphynx - GB 5.2.1 - Traiphum Prungtaengkit

 From Traiphum Prungtaengkit, of Thailand, an Edge-turning Pyraminx! He calls it a Mastermorphynx. [T]
Also shown compared to a curvy Mastermorphix and a Pyraminx.
Edge-turning Order 2
Edge-turning HMT (No name.)

 An edge-turning HMT. Not made AFAIK.
Edge-turning Order 3+
Megamorphix

 The Megamorphix. Based on a 4x4x4 cube.

Made by Adam Zamora [T], Apollo [T], Curvy Megamorphix by Traiphum [T]

Megamorphix (4-Layer Mastermorphix)

 Megamorphix (Stickerless version) - released by Moyu
Centerless Megamorphix - GB 5.2.4

 A Centerless Megamorphix.
Ultramorphix

 Ultramorphix - based on a 5x5x5 cube.

Made by Danny [T], Traiphum [T], judochiou625 [T]

Traiphum has made many orders of curvy morphix [T] - 6x6x6 "HexaPhobic" [T]; 7x7x7 [T]

Shengshou / Sengso 5-Layer Mastermorphix - Ultramorphix

Ultramorphix - Shengshou (5-Layer Mastermorphix) Ultramorphix - Shengshou (5-Layer Mastermorphix)

A mass-produced Ultramorphix - the 5-Layer Mastermorphix by Shengshou / Sengso. Stickerless version.
Shengshou / Sengso 6-Layer Mastermorphix - Hexaphobic

 A mass-produced "Hexaphobic" - the 6-Layer Mastermorphix by Shengshou / Sengso. Stickerless version.
Shengshou / Sengso 7-Layer Mastermorphix

 A mass-produced 7-Layer Mastermorphix by Shengshou / Sengso. Stickerless version.
Shengshou / Sengso 8-Layer Mastermorphix

 A mass-produced 8-Layer Mastermorphix by Shengshou / Sengso. Stickerless version.
Shengshou / Sengso 9-Layer Mastermorphix

 A mass-produced 9-Layer Mastermorphix by Shengshou / Sengso. Stickerless version.
Shengshou / Sengso 10-Layer Mastermorphix

 A mass-produced 10-Layer Mastermorphix by Shengshou / Sengso. Stickerless version.
Hybrid
Combominx

 Combominx - a custom 3D-printed twisty puzzle designed and made by Ben Streeter. [T]
It is a tetrahedral puzzle similar in appearance to the traditional Pyraminx -
it allows vertex turns but the trivial tips do not turn. It also allows edge turns!
Successive edge turns allow shapeshifting, and Pyraminx/vertex turns work in the shapeshifted form.
This puzzle is fairly large, but needs to be in order to accommodate the necessary mechanism -
even at this scale, the arms anchoring the tips are very thin.
It turns well and smoothly, without lockups, and is very stable - I love it!
Ben posts as benpuzzles - check out the benpuzzles YouTube channel, and Ben's i.materialise shop.
Having some time ago acquired a custom edge-turning (only) Pyraminx, called the Mastermorphynx,
made for me by Traiphum Prungtaengkit, of Thailand,
I knew I had to add Ben's hybrid to my twisty zoo!
Geared
Gear Pyraminx - Timur - Meffert

 Gear Pyraminx - from Meffert's, design by Timur Evbatyrov
(I have black and white versions.) Also a Series II in black.
Gear Mastermorphix

 A Gear Mastermorphix
Circle / Crazy
Crazy Tetrahedron - Mf8 / DaYan

 Mf8 DaYan Crazy Tetrahedron (Jupiter)
also Standard version (all circles turn with opposite vertex).
There are several versions.

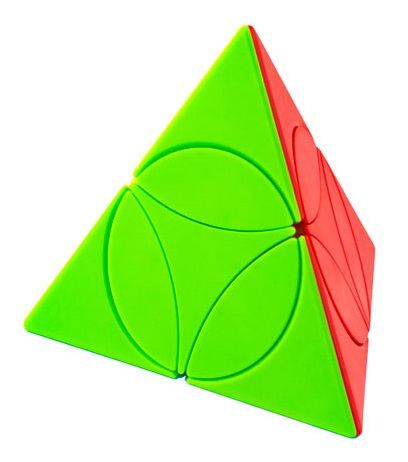
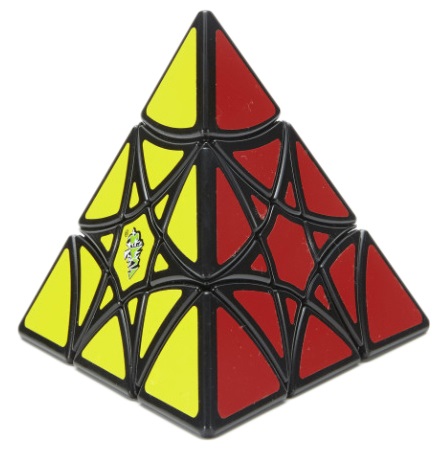
Petal Pyramid - Yongjun

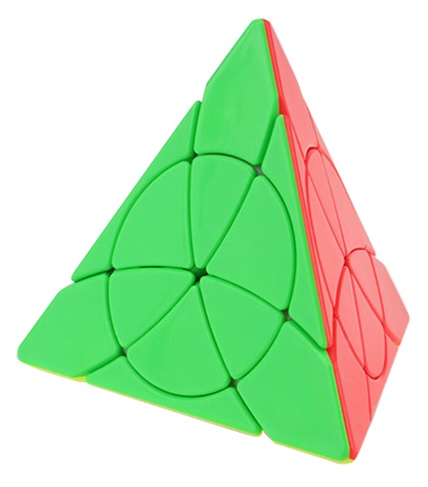
 Petal Pyramid - Yongjun
Vertex/face turning like the Pryaminx, but without trivial tips. The face disks rotate in place, mixing "tip segments" and "edge segments" among their own kind.
Solving the Petal Pyramid
  1. Solve the tips and outer edges just like a Pyraminx.
  2. Solve the tip segments intuitively.
  3. Solve the edge segments. You can swap two using the algorithm shown here.

To swap the edge segments at A and B assuming they are opposing colors, hold the puzzle as shown and perform this sequence, where R means turn the R corner 120 degrees clockwise (R' ccw) and T means turn the top inner circle 120 degrees clockwise (T' ccw):

R T R' T'
R T R' T
R T' R'

NOTE that this is really a 3-cycle moving A->c->B->A. When A and c start as the color of T, the A->c part is masked. B moves to A as intended, and c->B restores B to the T color. Got it? If you perform this when both faces are already solved, it appears to swap A and c. To go the opposite way, change that 3rd T to T'.

Coin Tetrahedron (Coin Pyramid / Coin Pyraminx) - QiYi

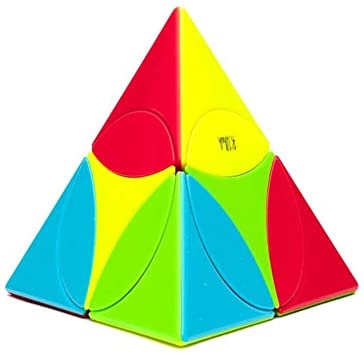
 Coin Tetrahedron (Coin Pyramid / Coin Pyraminx) - QiYi
The face disks rotate in place, mixing the oval segments on a face. When the face discs with their three oval segments are properly aligned, the vertices can be turned, each permuting three oval segments. This puzzle is very easy to solve.
Related
Starburst

 The Starburst has been mass produced, but was also a common custom mod of a Pyramorphix - Just add tetrahedrons to the "empty" triangular faces (they do not rotate in place).
Vulcano / Trignis - Timur / Meffert

 From Meffert's, the Vulcano (aka Trignis) designed by Timur Evbatyrov.
Dinomorphix - Traiphum

 Dinomorphix - designed by Traiphumi, produced by Calvin Fan [T] [T]

A hybrid face-turning and vertex-turning puzzle - each of the four faces turns like a Babyface puzzle. In addition, each of the four vertices can turn, like the trivial-tipped puzzles with this cut pattern, but since the faces also turn, the corners are tri-partite, making them non-trivial.

Fun fact: I helped Triaphum choose the name for this puzzle!

Platypus / Jackpot / NGP (New Generation Puzzle) - Meffert

 Mefferts Jackpot and NGP. Designed by Yusuf Seyhan. Patented back in 2003.

Same turning regime as Triaphum's Dinomorphix - the faces turn, and the tripartite tips turn. Issued prior to the Dinomorphix. However, unlike the Dinomorphix, there are hexagonal face-centers and the tips have triangular faces - both of which show orientation that can matter. There are several variations and knock-offs. [W] [W] [W] [W]

Jaap says these are related to the Dino Cube, which is very easy to solve. Jaap's page.

Ghost Pyraminx - Lefun

 Ghost Pyraminx - Lefun
Actually this is a Ghost HMT.
Gemini Pyraminx (Binary Star Pyraminx) - Lefun

 Gemini Pyraminx (Binary Star Pyraminx) - Lefun
Star Pyraminx - Lanlan

 Star Pyraminx - Lanlan
Curvy Clover Pyraminx - Lanlan

 Curvy Clover Pyraminx - Lanlan

Hexahedral (Cubic) Twisties

FVE
O1O2O3+O1O2O3+O1O2O3+



















 

Face-turning Order 1
Rubik's 2x2x2 Pocket Cube - GB 3.1.1
3.7*106 = 3,674,160 - Erno Rubik; 6-armed spider.

Rubik's Pocket Cube

Jaap's page

Solve using a subset of the 3x3x3 algs.

Algs to finish bottom corners
(begin by positioning 2 or 4):
Swap adjacent front bottom corners: {R'D' R F} D {F'R' D R} D2
Swap front left bottom diagonally: {R'D' R F} D2 {F'R' D R} D
Leave front left, turn other 3 CCW: R' D' R D' - R' D2 R D2
CW (inverse of above):
D2 R' D2 R - D R' D R

Various 2x2x2 Cubes


Rubik's Pocket Cube, Studio Mini Cube, Ice Cube, Yuxin 2x2x2, V-Cube V-2, New Spring clear (with transparent stickers), and a version with interior tinted pieces


Rubik's Soft Cube
A fully functional 2x2x2, about 4" on a side, with fabric-covered soft cubies.

Bump Cube Jr.

 Asymmetric spacing of cuts results in the Bump Cube Jr. made by Thomas [T]
2x2x2 Mirror Blocks

 A mass-produced 2x2x2 Mirror Blocks Cube
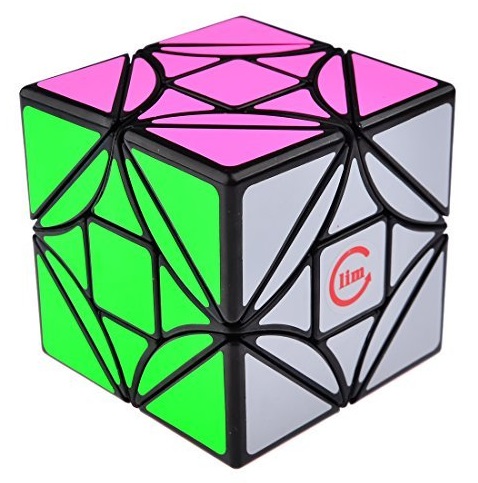
2x2x2 Ghost Cube

 Ghost Cube 2x2x2
produced by Lim Cube
Os Cube

 Os Cube - a clever 2x2x2 variant designed by Ilya Osipov, produced by QiYi.
A face turn causes internal magnetic components to either retract or extrude some facelets on the cubies. The goal is either to achieve the state where all facelets are retracted, or where all are extruded.
A novel mechanism that secured this puzzle a "Top Ten Vote Getters" award in the 2021 IPP Nob Yoshigahara Puzzle Design Competition.
Face-turning Order 2
The 3x3x3 Cube
4.325*1019 - Erno Rubik - 6-armed spider - BE887875

3x3x3
Rubik's Cube

Solving the 3x3x3

20 moves suffice!

In August of 2010, Morley Davidson, John Dethridge, Herbert Kociemba, and Tomas Rokicki proved that every scrambled position of Rubik's Cube can be solved in 20 moves or less. (Finding those 20 moves, however, can be quite a challenge!) Read more at www.cube20.org. In January of 1995, Michael Reid proved that the "Superflip" position (corners correct, all edges placed but flipped) requires 20 moves, so 20 was known to be a minimum.

See the Speedsolving.com Wiki.
Also see Ed Karrels' page.

I learned using a layer-by-layer (LBL) method:

  1. Top Edges (intuitively)
  2. Three Middle Edges (intuitively)
  3. Top Corners (intuitively, using unsolved middle edge as keyhole)
  4. 4th Middle Edge (2 algs)
  5. Permute Down Corners (2 algs)
  6. Orient Down Corners (1 alg + inverse)
  7. Permute Down Edges (3-cycle alg, optional Zperm & Hperm)
  8. Orient Down Edges (3 algs)

Step 4: move an edge from D to FL:
Start in FD matching F: D L D' L' - D' F' D F
Start in LD matching L: D' F' D F - D L D' L'

Step 5: permute D corners:
(begin by positioning 2 or 4):
Swap adjacent FD corners:
{ R'D' R F } D {F' R' D R} D2
Swap front right down diagonally:
{R'D' R F} D2 {F'R' D R} D'

Step 6: orient D corners:
Leave front left, turn other 3 CCW: R' D' R D' - R' D2 R D2
CW (inverse of above):
D2 R' D2 R - D R' D R

Step 7: permute D edges:
If an edge is already in position, hold it in DF.
clockwise (viewed from bottom) 3-cycle of DL->DR->DB: L'R - F - LR' - D2 - L'R - F - LR'
aka, where ( means L'R, and ) means LR':
(F)D2(F)

counterclockwise: (F')D2(F')

You can always use the 3-cycle repeatedly, but here are a couple of shortcuts:

Zperm - swap DF-DL and DR-DB:
(M = middle vertical layer, same dir. as L)
M'D' M2D' M2D' M'D2 M2D

Hperm - swap DF-DB and DR-DL:
M2D' M2D2 M2D' M2

Step 8: orient last edges:

Flip FU and FR in place:
R'D'L' { U' F' U F'} L D R { U F U' F }

Flip FU and FD in place:
{ U' F' U F' } L D R { U F U' F } R'D'L'

Flip all four D edges in place:
(F2) D2 (F) D2 (F2) D'

Here are some extra algs:

Superflip (every edge flipped in place) algs - see Michael Reid's page, Walter Randelshofer. Here is one:
U R2 F B R B2 R U2 L B2 R U' D' R2 F R' L B2 U2 F2

Here is the checkerboard pattern:
U2 D2 F2 B2 R2 L2

Other patterns: Michael Reid.

"Six Spot" - U D' R L' F B' U D'
Cube in cube - F L F U' R U F2 L2 U' L' B D' B' L2 U

Various Rubik-brand 3x3x3 Cubes
Various 3x3x3 Speedcubes
Notes on speedcubes
(Be advised that it has been quite some time since I compiled this info. The world of speedcubes and the available models have continued to evolve so my info is out of date.)
Types I have are highlighted like this.
Types I have and prefer are highlighted like this.
Rubik's Brand
  • Regular Rubik's storebought
  • 25th Anniv. Cube
  • Rubik's Icon Cube
  • Rubik's Studio Cube
  • Rubik's Cube Deluxe (tiled)
  • Rubik's Game
  • Rubiks.com DIY 3x3 Assembly Cube
  • Politoys Cube
  • Rubik's brand Japanese speed cubing kit - JSK
  • (There is also a JSK clone.)
Chinese Cubes - Type A

All Type As are designed and manufactured by the Chinese company "Guo Jia." There are two sets of Type A’s - the second set has the extra designation "quanfeng" which means “all sealed.”

  • Type A I (or "old"): GuoJia
  • Type A II: GuoJia 2
  • Type A III: GuoJia QuanFengBi
  • Type A IV: parts come on trees - plastic washers - IV has tracks on edge piece, V does not; fragile corners, non-cubic edges
  • Type A V
Other Chinese Cubes

  • Type B: GuoYi (made by ShengEn)
  • Type C: GuoBing (Rubik's DIY replica)
  • Type CII - sealed
  • Type D: GuoYou (made by YongJun, a.k.a. YUGA)
  • Type DII - YUGA II - sealed
  • Type E (Diansheng no.222)
  • Type E (Diansheng no.333)
  • Mini Diansheng
  • Type F: GuoYi BanFengBi (made by ShengEn)
  • Type FII - sealed
  • Type G (hknowstore)
Other Speedcubes

  • Cubeforyou.com brand DIY
  • Ghost Hand Cube (aka Popbuying Fingertip Dancing)
  • Magic Cube
  • Ming Ho (see hknowstore)
  • Clown Cube ("Revenge Cube" with clown picture on package insert; 8906B; painted "stickers")
  • Slick Cube - www.slickcube.com (type D clone?)
  • HeShu (see kcobe.com)
  • Edison Cube (Korean)
  • Joy Cube (Korean)
  • DAISO (1 dollar store) - painted - fake type F
  • Haiyan cubes - Haiyan Zhuang holds a blindfolded world record - www.cubehaiyan.com
  • Haiyan's cube - Memory = New Type A V + Sanding
  • Haiyan's cube - Haiyan = Haiyan's New Cube
  • DaYan I Tai Yan (aka Big Goose)
  • DaYan II GuHong Cube - allows reverse corner cuts - my old favorite 3x3x3!
  • DaYan III LingYun - even better than the GuHong II.
  • DaYan IV LunHui - after re-tensioning and lubing, my new favorite - even better than the ZhanChi V
  • DaYan V ZhanChi - a great cube right out of the box
  • CUNI 3x3x3 with metal internals by Alpha Cube

The Chinese twisty puzzle company DaYan has offered a series of five 3x3x3 cubes, each with a different internal design.
I took this comparison photo showing an edge piece and corner piece from each, to help keep them straight.
From left to right: 1 Tai Yan (Big Goose); 2 GuHong; 3 Ling Yun; 4 Lun Hui; 5 ZhanChi.
My current favorite is the DaYan 4 Lun Hui.

Face-turning Order 2 with Feature Modifications (not Shapemods)
Bump Cube / Rubik's Mirror Blocks - Hidetoshi Takeji

 Rubik's Mirror Blocks (aka Bump Cube)
designed by Hidetoshi Takeji.
The Bump Cube was entered in the IPP 2006 Design Competition. The hand-crafted version had been for sale at $320.
I got a mass-produced boxed copy signed by Hidetoshi-san.

A key innovation and variation on Rubik's theme - in this case, you don't solve by color. Rather, the center has been offset so that every piece's three dimensions differ from every other piece's dimensions. The cube must be solved according to shape! When scrambled, it becomes a bumpy mess that can be very confusing on first encounter. Fortunately, it can be solved using the same algorithms developed for Rubik's Cube.

Hanzoh aka Half-turn Cube - Oskar van Deventer

 Hanzoh aka Half-turn Cube produced by Oskar [T], also made by Hidetoshi Takeji [T], based on an idea by Takafumi Haseda
Void Cube - Katsuhiko Okamoto
1/12 of a normal 33; 3.60*1018 - Katsuhiko Okamoto

The Void Cube, designed by Katsuhiko Okamoto.
Manufactured by Gentosha Toys. Purchased from Torito.

Also a more recent Rubik's Void.

The Void Cube won the Jury Grand Prize in the IPP 2007 Design Competition.

It is kind of an "inside joke" for cube fans who know how the original Rubik's 3x3x3 internal mechanism works by employing a six-armed spider fixed to the centers. The Void cube has no centers and no internal spider! How do the pieces stay together? A design triumph. Spawned other "holey" designs - e.g. the Holey Megaminx, the Holey Skewb.

When solving the Void Cube, you might run across a parity problem.

To see the internals, see this thread on TwistyPuzzles.

Edges-only 3x3x3 - Smaz

 An Edges-Only cube from "Smaz."
Edges-only Void 3x3x3

 An Edges-Only Void cube.
Simple Overlapping 3x3x3 - Kevin Phelan

 I received a pleasant surprise in the post, in the form of this great Simple Overlapping Cube twisty puzzle, cleverly made by TP forum member "Zzupler" (Kevin Phelan, of Ireland) [T], and originally designed by David Calvo [T].

This "corners-only" 3x3x3 is kind of the brother to the "edges-only" 3x3x3 above.

It is nicely done and turns very smoothly. Thanks, Kevin!

Brilicube


 The Brilicube. Originally designed by Aleh Hladzilin. [T]
It is a 3x3x3 cube with hidden face centers.
This version purchased from the Shapeways shop of "grigr." [T]
This is the first Shapeways puzzle I got in black strong flexible material.
It started very tight and difficult to move, but is better after much wearing of the pieces, and lubrication.
Face-turning Order 3+

 

4x4x4
7.4*1045 - Peter Sebesteny - grooved sphere

4x4x4
Rubik's Revenge
Eastsheen A4 (a different mechanism)
Maru 4x4x4
Shengshou 4x4x4
Ghost Hand 4x4x4
QJ Pillowed 4x4x4
Moyu Aosu 4x4x4 stickerless

There are now several 4x4x4 mechanisms available - some of which are superior to the original Revenge, which is very stiff and prone to the center stems breaking.
  • Original Rubik's Revenge
  • Eastsheen - turns smoothly but catches
  • Meffert's
  • QJ (aka "Clefferts" - a clone of the Mefferts)
  • Maru (similar to V-6 mech)
  • Mf8/DaYan
  • Lanlan (similar to QJ)
  • Shengshou 4x4
  • Ghost hand 4x4 II (similar to Shengshou)
  • X-Cube 4x4 (has "Pi mod" - core stays aligned)
Solving the 4x4x4

Method: Reduction to 3x3x3

Steps:
1) Solve centers
2) Pair up edges
3) Solve as 3x3x3
  a) Top Cross
  b) 3 of the 4 vertical edges
  c) using last vert edge as keyhole, solve top corners
  d) last vertical edge
  e) permute bottom corners
  f) orient bottom corners
  g) permute bottom edges - MAY HAVE PARITY
  h) orient bottom edges - MAY HAVE PARITY

Solve centers - Intuitively -
a) move a desired center from F or D to U - pre-rotate U so you will DISPLACE 1 or 2 correct centers already in U
b) rotate desired center into U using l' or r (if from F), or l2 or r2 (if from D)
c) do U or U2 to save the newly placed center
d) fix D centers by undoing the rotate-in move you made in (b)
repeat until all centers done - make sure to get colors right
(w first, then y opposite, then r anywhere, then b clockwise from r,w - then g opposite b)

Pair up edges
repeat until all edges are paired (except for maybe the last pair of edge pairs):
a) pair the FLU upper left vertical front edge piece -
rotate so at least one mismatched pair is in UF or UB or UR, and FL
b) move FLU's mate into FRD
c) do d' (or D'd') to move mate next to FLU
d) do L' to move new matched pair to U
e) rotate U to replace matched pair with an unmatched pair
f) do L
g) do d (or Dd) to restore F centers
stop if all edges are paired, or if last two unmatched pairs remain, else go to (a)
move last two unmatched pairs into FLU/D and FRU/D - they will either be straight across from each other or diagonally across
if diagonal, swap them so they are straight across - use:
L' R U F U' L

When straight across, do:
Dd R F' U R' F D'd'

NOW use 3x3x3 algs for solving steps 3a through 3f.
NOTE that there shouldn't be problems solving the corners

Use 3x3x3 algs for steps 3g and 3h, too - BUT there may be parity problems.
Two extra algs to solve edge parity problems:

To swap UF with UB edge pairs:
r2 U2 r2 U2 u2 r2 u2

To flip UF edge pair:
r2 BACK2   U2 l U2 r'   U2 r U2   F2 r F2 l'   BACK2 r2

If it seems like it's not working, it's probably because you're mistakenly doing D2 (DOWN) rather than B2 (BACK), or R and L rather than r and l! Mind those lower-case inner slice moves!

DONE!

5x5x5
2.8*1074 - Udo Krell - 6-armed spider

5x5x5
Rubik's Wahn
Professor Cube
Eastsheen A5 (a different mechanism)
QJ Pillowed 5x5x5

6x6x6
1.57*10116 - Panagiotis Verdes

6x6x6
V-Cube 6
from Verdes Innovations.

7x7x7
1.95*10160 - Panagiotis Verdes

7x7x7
V-Cube 7
from Verdes Innovations.

Verdes worked diligently over several years to finally come up with an internal mechanism that would allow cubes beyond 5x5x5 to be made. Prior to their achievement, most assumed this would be impossible due to fundamental geometrical limitations of the spherical cutting patterns employed inside the cube mechanism. Basically, as the cube grew larger to accommodate more edge pieces, some pieces would no longer have any way to connect to the core. Verdes' design ideas are the subject of a key patent. There have been several alleged infringements, coming out of Asia. Verdes has produced a 6x6x6 and 7x7x7, but even though their method allows up to an 11x11x11, only clones exist beyond 7x7x7. You can find 8x8x8, 9x9x9, and 11x11x11 online. They are controversial among collectors because of the perception of disrespect to Verdes. As an exercise in what is possible, Oskar van Deventer produced a 17x17x17 of his own design, called "Over the Top." [Y] [S] [W]

Vertex-turning Order 1
Skewb - GB 3.2.1

Modern Speed Skewbs
3.1*106 = 3,149,280 - Tony Durham

The Skewb - The order-1 vertex-turning cube
(Mefferts stickered and tiled versions)

Modern Speed Skewbs
Shengshou Skewb (white), QiYi QiCheng stickerless Skewb, Cong's Design MeiCheng stickerless Skewb, Moyu Magnetic stickerless Skewb
My favorite is the QiYi QiCheng stickerless Skewb.

Solving the Skewb
Jaap's page
Meffert's solution

Hold the Skewb with one face towards you. The upper right corner is R, and the upper left corner is L.

The ONLY algorithm you need is the "Sledgehammer" (SH)
R' L R L' (remember the rhythm down down up up)

Also, y2 means spin the whole cube around its vertical axis 180 degrees so its back faces you.

  1. Pick a start face - usually white. Hold it on top. Place its corners - intuitively.

  2. Flip the cube over so the solved (white) face is on the bottom
    and next solve the other four corners (yellow) now on top - this needs at most two steps:

    A) If none of the yellow sides of those corners are up, then hold the cube so
    the two that are on the same side (the "headlights") are towards the right, and do SH

    B) If two yellow sides of those corners are up diagonally across from each other,
    hold the cube so they are pointing NE and SW,
    and one yellow corner facelet is on the front in the upper right. Do SH then go to (A).

  3. Place the face that goes with those corners (yellow) -
    Hold yellow corners up, hold yellow face in back, do:
    SH y2 SH

  4. The top and bottom faces have been solved - possibly others, too.
    We're going to use the 3-cycle F -> B -> U -> F to solve the remaining faces.
    Hold two solved faces at L and R. If a 3rd face is also solved, hold it at D.
    If possible, also hold the cube so that at least one of the steps in the 3-cycle will put a face where it belongs.
    Perform SH y2 SH and re-do this step as needed.
Holey Skewb / Void Skewb

 Holey Skewb twins from Meffert (designed by Tony Fisher)
Meffert's Pillowed Holey Skewb, in black, from PuzzleMaster
Double Skewb - Moyu Meilong

 Double Skewb - designed by Guan Yang, produced by Moyu Meilong
It may look like the Holey Skewb, but this variant has an internal colored core visible through the face openings, that will turn in conjunction with various Skewb moves, behaving like a Pyraminx. A solved cube must also restore the proper arrangement of the internal colors.
Asymmetrically cut Skewbs

 Asymmetric spacing of cuts, or asymmetric cuttings, results in different families of puzzles, such as Okamoto's Offset Skewb.
Container Cube (Skewb)

 Container Cube - originally a custom Skewb mod by Tony Fisher, now mass-produced by Moyu
Fisher Skewb - Moyu

 Fisher Skewb - Moyu
Designed by Nathan Wilson
Vertex-turning Order 2
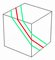
Just as with the O2 tetrahedral puzzles, three basic O2 VT forms arise as the two O2 cuts (blue) are moved away from (or toward) the original Skewb cut (red).
In these O2 puzzles, the blue cuts are present but the red Skewb cut is not.
3.2.2 Master Skewb 3.2.4 Dino
also Cubocta = Rainbow Cube
Oskar's Redi Cube is a Dino with visible corners 		Compy Cube
idea by Wayne Johnson [T], realized by Jason Smith [T], earlier paper model by Robert Webb [T]; Curvy Dino by Evgeniy

Carl Hoff introduced a clever animation [T] he calls an "order-2 corner-turning multicube" - it shows how moving cuts define different puzzles of the same order.
Carl shows the cuts moving inwards from trivial tips, converging on the single skewb cut, which the animation stops before reaching:

Compy Type
Compy Cube - Jason Smith

 I bought one of the large versions of Jason Smith's first run of the Compy Cube. [T] [T] The Compy Cube (aka Shallow Dino, aka Sausage's Cube) is a full custom 3-D print. It is easy to solve intuitively, requiring no memorized algorithms. I dyed my Compy Cube purple, just to be different.
Curvy Dino

 Curvy Dino - designed by Evgeniy Grigoriev, issued by Calvin's Puzzle
Same as a Compy Cube.
Dino Type
Dino Cube - GB 3.2.4

There are four sticker-variations of the original vintage Dino Cube:


2 colors
312.55/1
4 colors
42,000 states
528.99/1;535.55/1

6 colors, no dinos
337/1
6 colors, with dinos
1.9*107 states
667.96/1


James R. Holloway 1995
U.S. patent 6056290

I have an original boxed four-color version. (I traded another one to Kevin Uhrik for a Master Octahedron.) The Dino has been re-issued by Smaz, who provided the version with the attractive hollow stickers. I also got a version with repro Dino stickers.
I got a pillowed void dino cube from Calvin.

There are many cheap modern versions available - I got a stickerless Sengso Legend 8 Axis Dino Skewb.

Rainbow Cube
2.4*108 = 239,500,800 - Bethel Japan

Rainbow Cube
Comes in 7-color and 14-color versions.
Very easy to solve intuitively.
Jaap's page

When the Dino Cube became scarce, the Rainbow Cube was a good substitute - they are basically the same puzzle - the Rainbow Cube is a cuboctahedral form of the Dino. A common mod was to transform a Rainbow back into a Dino. Original Bethel Rainbow Cubes are now rare in their own right.

Dino Cylinder - Smaz

 Hong Kong puzzle designer and craftsman Smaz has mass-produced his Dino Cylinder design [T] [T]. His original "hollow" stickers make for a beautiful puzzle! It is even shipped in a nice black velour drawstring bag.

This puzzle solves like a Dino or Rainbow and is fairly easy. However, unlike the Dino, this puzzle exposes corner pieces each of which can be independently oriented in one of 3 positions. Using the same notation I used for the Mosaic Cube, here is an algorithm to rotate the df corner clockwise by 120 degrees:

ur' df' dr' -- df dr ur -- uf df uf'

In the second photo, I have applied this to all eight corners.

Redi Cube - Oskar van Deventer

 The Redi Cube by Oskar van Deventer
Originally a custom 3D print, now mass-produced by Moyu
Essentially a Dino with visible corners
It is easy to solve intuitively - the only difficult step might be to rotate a single corner 120 degrees. Really this amounts to a 3-cycle on the pieces surrounding that corner - use an edge adjacent to an adjacent corner as a parking place.
8 Petals Cube - Yuxin

8 Petals Cube - Yuxin 8 Petals Cube - Yuxin

8 Petals Cube - Yuxin
Essentially the same as a Redi Cube.
Honey Copter - Lanlan

Honey Copter Honey Copter

Honey Copter - LanLan
Essentially the same as a Redi Cube.
X-Box Cube - Pitcher

 X-Box Cube - designed by Dave Pitcher, made by Chewie's Custom Puzzles
A variant of the vertex-turning Dino Cube, where corners are prominent but as usual do not permute.
Simple but I like it.
Essentially the same as a Redi Cube, and in turn very similar to the Honey Copter.
Master Skewb Type
Master Skewb - GB 3.2.2 - LanLan

 Lanlan Master Skewb in black (also have one in white)

This is a relative of the FTO, and the Rex Cube is in turn a relative of this.

Here is a diagram by "Allagem" (Matt Galla) [T] showing how the Master Skewb and FTO are similar:

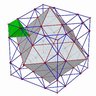
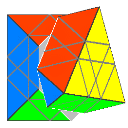
The MS corners have no equivalent on the FTO, but they do have equivalents (the face centers) on GB 4.1.4 [T].

Master Skewb - GB 3.2.2 - "Cublem"

 A pillowed white Master Skewb made by TP forums member "Cublem" [T]

I bought this before the LanLan mass-produced version came out. It wasn't the first or the last time I have bought an expensive hand-made (or 3D printed) puzzle only to see an inexpensive mass-produced version appear later. Most collectors run this risk and accept it.

Rex Cube - GB 3.2.6 - Drew Cormier

 Drew Cormier's Rex Cube [T]
is equivalent to a cornerless Master Skewb [T].
First designed by Drew Cormier back in early 2009 [T] [Y], then produced commercially (without his knowledge) [T].
Now offered via Meffert, with a royalty going to Drew.

Drew's Praxis Cube (I don't have) is an "axised" Rex. [T]

Super Ivy Cube - QiYi

 Super Ivy Cube - from Qiyi. Equivalent to the Rex Cube.

Solving the Rex Cube / Super Ivy Cube

Please refer to the annotated diagram.

To avoid parity, ensure you know the solved face color order clockwise around a given vertex, and which colors oppose each other. In my case I always remember vertex "F" and that the colors clockwise around that corner are red, white, and blue in order. I also remember that the opposite pairs are red/orange, white/yellow, and blue/green.

As is usually the rule for vertex-turning puzzles, solving this puzzle is not overly complex. The process comprises three main phases, and the first two can often be done intuitively, but I will include some useful operators for the first two phases here along with the key operator for the final phase.

The puzzle has three visible piece types:

  • edges such as 1, 2, 3, and 4
  • face centers such as X, Y, and Z
  • and "petals" such as a, b, m, and n.

A move consists of turning a vertex such as R, L, F, or D 120 degrees clockwise or counterclockwise as seen when looking directly at it (the former move indicated by the corner's letter, the latter by the letter followed by a single quote, pronounced "prime"). An operator is a sequence of such moves, perhaps including a rotation of the entire cube about some axis.

I think another interesting visual feature of this puzzle is a group of three pieces - a face center plus two adjacent, opposite, petals, which together resemble an "eye" (or an American football) - such as the group a, X, b. What's interesting is that any single (vertex) move displaces three eyes, each of which moves as a unit.

The solving phases are:

  1. Position the edges (while doing so ignore the other piece types)
  2. Position the face centers (while doing so, ignore the petals, but keep the edges solved)
  3. Swap petals until all are correctly placed and the entire puzzle is solved. Using the associated algorithm judiciously will ensure the edges and faces previously solved remain so - and this is where most of the puzzling fun comes in.
To start, place edges 1, 2, and 3 - intuitively. Your intent is to reconstruct your correctly colored starting vertex F. This should not be any real challenge.
Continue by placing the two remaining top edges, followed by the three remaining "vertical" edges - respecting what you know about the proper color pairing.

To properly place the last four edges of the bottom face (orange for me), you can flip the cube over so that face is on top and use the following algorithm.
To 3-cycle edges 1->2->4->1, do: F' L F L'
You can always reverse the cycle if needed by using the inverse sequence L F' L' F

After all the edges are in place, it should be clear where each color of face center belongs. Using the following algorithms to position the face centers correctly:
To 3-cycle face centers X->Y->Z->X (i.e. clockwise around F), do: L' R L R'
To cycle them counterclockwise, invert it: R L' R' L

Another useful algorithm will allow you to instead 3-cycle the face opposite Z, to Y, Y to Z, and Z backwards: L R L' R'
Of course, you may find it useful to invert that one, too: R L R' L'

Now we're left with the petals. Here's where it gets interesting - you really need only one remaining algorithm, but to be successful you'll have to learn to do and undo setup moves, and recognize when the operator can be safely used versus when it will have unintended consequences. Improvement comes with practice, trust me.

What the algorithm/operator does, is swap the two independent pairs of petals a<->b simultaneously with m<->n. (It also happens to rotate the face centers X and Z in place, but the coloring of this puzzle makes that invisible.) Note that when a and b are the same color to begin with, swapping them is essentially a no-op, again because of the coloring of this puzzle. This fact will become important later when you have to strategize how to do a single swap without messing up something else.

Here is the algorithm - it may be a bit confusing at first since it entails a step where you rotate the whole cube, which "re-labels" the vertices: to swap the two independent pairs of petals a<->b simultaneously with m<->n, do:
R L' R' L,
rotate the whole cube 120 degrees clockwise about the diagonal axis looking down at F,
L' R L R'

You'll probably have to practice that until it becomes natural and you can complete it without losing track of where you are. If the rotation and resultant re-labeling is throwing you, here's the sequence without doing the cube rotation around F: R L' R' L D' L D L'
It's just that fiddling with vertex D is awkward - it's better to flip the cube midway through so X becomes the top, which then makes L become R, and D become L, so you can just keep manipulating the top left and right vertices.

Regarding the setups I mentioned - notice that if before performing this algorithm, you first do F, that you end up swapping a and m. Then you could undo the previous F (do F') and the result is you've moved the a petal onto the Z face (and the m petal onto the X face). Of course there are other consequences - you've also brought the front petal from the Y face into play and will swap it with n! That is, unless you notice that this operator does not affect the three sides not seen here! So, be on the lookout for the opportunity to re-orient the cube so you can do the desired a<->m swap but so that the inevitable simultaneous swap affects two petals which either are already equivalent, or haven't yet been solved anyway.

Multi Skewb
Multi Skewb - designed by Gregoire Pfennig, produced by YuXin
I got a limited edition purple.
Asymmetric Vertex-turning Order 2
Dino Skewb / F-Skewb

 Dino Skewb (F-Skewb) - designed by Timur Evbatyrov, produced by DaYan

An order-2 vertex-turning, asymmetric puzzle - corners with small tips do Dino turns with their neighboring 3 square face pieces and 3 edge pieces, as well as Skewb-like turns with the further layer that move more than half the cube; corners with large 3-part tips are part of Skewb-like turns only that move less than half the cube.

DaYan Master F-Skewb

 DaYan Master F-Skewb (black)
Vertex-turning Order 3
The O3 VT combines the Skewb w/ each O2 VT form.
In these O3 puzzles, the blue cuts are present along with the red Skewb cut.
Skewb + Master Skewb
Elite Skewb - GB 3.2.3 - Eric Vergo, Drew Cormier

 This is the order-3 vertex-turning cube - GB 3.2.3 - a Skewb combined with a Master Skewb. It is called the "Elite Skewb" (but could also be a "Professor Skewb").

First made by Drew Cormier [T].

Eric Vergo made this Elite Skewb for me [T]. It's instance #1!

Elite Skewb - Mf8

 Elite Skewb - mass-produced by Mf8
Skewb + Dino
Dino Skewb - GB 3.2.5 - Tom van der Zanden

 Dino Skewb by TomZ [T] [W] [S]
Skewb + Compy
Compy Skewb - Tom van der Zanden

 TomZ's Compy Skewb [T] [Y]
Skewb + Compy
Compy Skewb - DaYan

 DaYan's "7x7" Skewb - aka Compy Skewb
This mass-produced version differs slightly from Tom's version in that here the small corners are trivial and rotate freely. In Tom's version, they are bound to the Skewb rotation, making Tom's version more difficult.
The next diagonal cut in from the trivial tip cut is the skewb cut for the opposite corner.
This puzzle does not allow the "Lattice Cube" type turns of a corner plus its immediately adjacent face and edge pieces.
The next cut is the compy cut.
Vertex-turning Order 4
(Order 4) Lattice Cube / Master Dino - GB 3.2.7 - Okamoto, Bedard, Pfennig

 GB 3.2.7 is an order 4 vertex-turning cube - a Dino with tri-partite vertices. Called the Lattice Cube or Master Dino - originally designed and hand-made by Katsuhiko Okamoto.
Later made by Scott Bedard [T] [Y] and Gregoire Pfennig, now mass-produced by Calvin Fan
(Order 4) Mosaic Cube (Fadi Cube) - Oskar van Deventer - Meffert

The Mosaic (Fadi) Cube (Meffert/Oskar van Deventer) is a Lattice with visible corners.

The mass-produced Mosaic Cube issued by Meffert was designed by Oskar van Deventer and originally available from Oskar's Shapeways Shop as the Fadi Cube. It is a vertex-turning, order-4 cube, related to Okamoto's Lattice Cube. There has been some controversy about the stability of the Mosaic Cube [T] and Oskar designed a new spherical core.
I bought a black spherical core from Shapeways and modified a Mosaic Cube to swap out the standard core.

To access the screws and disassemble the puzzle, one must first remove the corner caps, which are glued on and have three small legs that fit into sockets in the underlying stem piece. An Exacto knife, used with care, is helpful to pry up the corners.

One or more legs might break when a cap is removed, however this is not catastrophic - you can use "Stik Tak," "Fun Tak," or a similar product to re-attach the corners so they remain easily removable.

After swapping in the spherical core and adjusting the screw/spring tensions, I find the puzzle very stable, playable, and enjoyable. The Mosaic Cube is not overly difficult to solve. It is similar to a Dino or Rainbow Cube, as one might expect.

The steps I employ are:

  1. Orient the corners - they are fixed in place so this step is trivial. Once the corners are oriented, the correct face colors are evident.
  2. Solve the small square centers. These centers are attached in pairs - a single piece provides a square center to two adjacent faces. There are 12 such pieces and they can be solved in the same way as Dino or Rainbow Cube edge pieces - intuitively.
  3. Solve the large edge pieces. There are 24 of them.
I have three algorithms that sometimes prove useful. To describe the algorithms and their effects, we have to agree on a notation for the Mosaic Cube - here is what I use. I hold the cube at an angle and look at it edge-on - the up and down faces are held parallel to the floor, and an edge is towards you. I label the 8 vertices using two letters describing their position: UF, DF, UR, DR, UL, DL, UB, DB - as shown in the image (DB isn't visible).

Any of the 24 large edge pieces can be identified by giving the labels of the two corners it lies between, with the adjacent corner first. For example, the large edge piece on the bottom in front would be DFUF while the piece above it would be UFDF.

A move is a twist of a vertex by 120 degrees either clockwise or counterclockwise from the point of view of looking directly at the vertex. A move can encompass just a corner and the 3 large edge pieces surrounding it, or those pieces plus the further "layer" including 3 more large edge pieces, and 3 center dual-pieces (accounting for six small square centers). I will symbolize the latter move, clockwise, using the relevant corner name - e.g. UF means twist the UF corner and the two layers surrounding it 120 degrees clockwise. UF' symbolizes the corresponding counterclockwise move. I will use the lowercase name of the corner to symbolize the "smaller" move of just twisting the corner and the 3 large edges surrounding it - e.g. uf and uf' for counterclockwise.

To 3-cycle DFUF => URUF => URDR, use:
UF' ur UF ur'

To twist just the single UF corner piece 120 degrees clockwise, use:
(UR uf UR' uf)*2

To 3-cycle the far edges about the UF corner clockwise - i.e. DFUF => ULUF => URUF, use:
ur UF' ur' UF' ur UF' ur'

I figured that one out myself :-) - I do a setup (ur UF' ur'), then use the previous 3-cycle UF' ur UF ur', then undo the setup (ur UF ur'), which strung together looks like:
(ur UF' ur') UF' ur UF ur' (ur UF ur')

The adjacent ur' ur near the end cancels out, and the resulting adjacent UF UF simplifies to UF' giving the concise 7-step algorithm.

Curvy Mosaic - LanLan

 Curvy Mosaic - mass-produced by LanLan
Equal to the Mosaic Cube.
4x4 Curvy Dino Cube - AJ

4x4 Curvy Dino Cube - AJ 4x4 Curvy Dino Cube - AJ

4x4 Curvy Dino Cube - AJ
Similar to the Lanlan Curvy Mosaic, but this has independent (trivial) corners and more importantly, tiny triangular pieces between the central teardrops.
Edge-turning Order 1
24 Cube / Little Chop - GB 3.3.7 - Matt Shepit

 24 Cube aka Little Chop - designed and made by Matt Shepit [T] [T] [Y]
also made (from Shepit's design) by Taylor [T], Karl-Heinz Diekmann [Y], Pantazis Houlis [Y]

Here we have one of the most elusive puzzles in the twisty zoo - what is known as the "24 Cube" or "Little Chop." [T] [Y]
Only a few have been produced, based on a design by Matt Shepit of New Zealand, but AFAIK none turn very smoothly. The design uses what is known as a "shells mechanism" and is very complex. To date AFAIK no-one has produced a viable alternative mechanism for this puzzle, and not for lack of trying. People have cheated by using a steel ball as a core and embedding magnets in the pieces, but such implementations don't work satisfyingly well. [S]

Chromium Cube - James Li (24 Cube / Little Chop - GB 3.3.7)

 Chromium Cube (24 Cube aka Little Chop) - designed by James Li
Mass-produced version - finally!
Not perfect - proper turning is difficult - but it is great to have this puzzle made available.
A rails mechanism using gravity pins to help prevent internal mis-alignment.
I bought two - regular stickers, and super stickers.
Edge-turning Order 2
Here is Carl Hoff's animated "order-2 edge-turning multicube" [T] which illustrates nicely how the spacing of the two cuts between pairs of opposing edges can be varied - in the Helicopter, the spacing is such that the layers touch but do not overlap. In 3.3.3 (Drew's Quad-X) the layers overlap and the spacing is symmetric. More and less overlap is possible, with different pieces [dis-]appearing.

Helicopter Cube - GB 3.3.1 - Okamoto, Cowan

 I am very pleased to have finally obtained a custom-made Helicopter Cube from Adam! The Helicopter Cube was first discussed in the TwistyPuzzles forums in thread 6253 - a particularly rich thread in which several ideas, including the concept of jumbling as opposed to shape-shifting, were broached. (More discussion on jumbling: 13071, 11126 .) Katsuhiko Okamoto mentions that he had completed his equivalent Bevel Cube the previous month. Robert Webb extrapolates a rhombic dodecahedral puzzle and Matt Shepit hints of its realization - it will be Shepit's Rua. Various folks have discussed their attempts to make their own Helicopter Cubes: 13856, 13520, 12030, 12423, 11679.

Helicopter Cube solution

Helicopter Cube - GB 3.3.1 - Meffert

 The Helicopter Cube has also been produced commercially. I bought a black one and a white one.
Helicopter Cuboctahedron - Garrett Ong, Eric Vergo

 Garrett Ong designed and Eric Vergo made an order-2 vertex-turning cuboctahedron, which is equivalent to a cuboctahedron Helicopter [T].
Partially Unbandaged Helicopter Cube - Eric Vergo

 A Partially Unbandaged Helicopter Cube designed by Eric Vergo [S] - this is copy number 1, obtained from Eric at NYPP2011.
When a jumbling move is made, a triangular face piece can swap places with a corner - this is not possible on the regular Helicopter Cube.

Vergo also made a 2x2x2 + unbandaged heli hybrid [T]

Curvy Copter - GB 3.3.0 - Tom van der Zanden - Meffert

 Meffert's is offering the mass-produced Curvy Copter created by Tom van der Zanden [T]. Tom's Curvy Copter has been very popular as a custom-produced 3D printed puzzle [S], and is now available at one tenth the price. I bought the black and white "twins" pair. The Curvy Copter functions like a Helicopter cube, but it exposes central edge pieces that must be correctly oriented, making it a more difficult challenge.
Lanlan's version is called the Butterfly cube.
Curvy Chop - Smaz

Curvy Chop - Smaz Curvy Chop - Smaz

The Curvy Chop by Smaz
Half of a curvy copter.
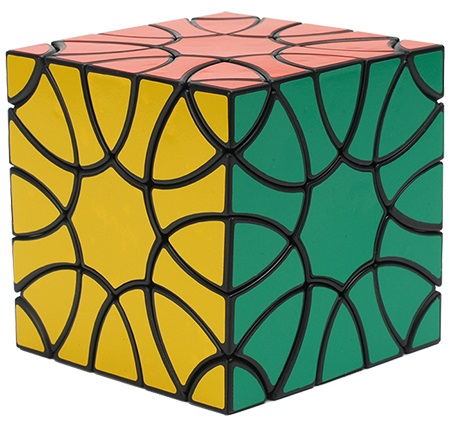
Clover Cube - QiYi

 QiYi Mofangge Clover Cube (stickerless) - designed by Yukang Wu.
A variant of the Curvy Copter.
Clover Cube Plus - QiYi

 QiYi Mofangge Clover Cube Plus (stickerless)
A variant of the Curvy Copter, hybridized with a 2x2x2.
Curvy Copter Plus - Tom van der Zanden

 TomZ's Curvy Copter Plus, mass-produced by Meffert [T] [S] has additional cuts that partially unbandage some turns
Curvy Copter II - GB 3.3.8 - Tom van der Zanden

 Curvy Copter II by Tom van der Zanden [T] [Y]
Curvy Copter III - Mf8

 Mf8 Curvy Copter III - stickerless version
Quad-X - GB 3.3.3 - Drew Cormier

 Drew's Quad-X [T] [Y] (cubic Rua)
DeCETH (Deeper Cut Edge-Turning Hexahedron) - Gregoire Pfennig

 DeCETH (Deeper Cut Edge-Turning Hexahedron) - Gregoire Pfennig [T] [Y]

Deeper cut than the Quad-X

Master Little Chop - Ben Streeter

 Master Little Chop - Ben Streeter [T] [Y]

Deeper still than the DeCETH

Hexaminx - Tony Fisher

 Fisher's Hexaminx (cubic Megaminx) [T]
Hexaminx - Pillowed version by Traiphum Prungtaengkit

 Pillowed Hexaminx from Traiphum Prungtaengkit, of Thailand [T]
(Shown with Helicopter Cube)

I traded this to Kevin Uhrik for a Tutt's Icosaminx.

Pillowed Hexaminx (mass-produced)

 A Pillowed Hexaminx - mass-produced by Calvin Fan;
this cubic shapemod of a dodecahedral Megaminx was first designed by Tony Fisher
then produced in a beautiful pillowed form by Traiphum Prungtaengkit.
Mini Hexaminx - Grégoire Pfennig

 Here is a Mini-Hexaminx, designed and made by Grégoire Pfennig, printed by Shapeways. [T] [S]
Shown in comparison to a U.S. quarter, a Pillowed Hexaminx hand-made (cast) by Traiphum Prungtaengkit, and a Tomy Megaminx.
This small wonder is very stable and usable. I am impressed that something so compact works so well. Nice work, Greg!
Edge-turning Order 3+
GB 3.3.12 - 24+Heli

 O3 would be 3.3.12 24+Heli
GB 3.3.16

 O4 3.3.16
Eitan's Master Helicopter - Eitan Cher

 O4 - Eitan's Master Helicopter - his first version was really a Master Curvy Copter [T] [T]

Eitan revised the design and also offers a "true" Master Helicopter (no exposed edge centers) [T] [Y] [T]

O1,O1 Hybrids
GB 3.4.1 - Skewb + 2x2x2 (aka Super-O, SuperZ, Skew-by-2, Skewb-by-2)

Attempted by several designers. None worked well enough to be sold, though...
  • Cowan [T]
  • timselkirk [T]
  • Eitan [T]
  • TomZ [T]
  • James Li [Y]
  • iaroslavski made a magnetic version [T]

BTW, Noah coined the term "Skew-by-2" but he meant something different: [T] - a Simple Overlapping 3x3x3 Cube, with the corner caps modified so the whole thing looks like a Skewb. It would twist like the SOC, not a Skewb.
"smashy" suggested the same thing and called it "Skewbik's Cube" [T]

GB 3.4.1 - Skewb + 2x2x2 - Limcube SuperZ

Limcube SuperZ

SuperZ - a mass-produced 2x2x2 + Skewb by Limcube
Very happy to be able to add a SuperZ to my twisty zoo!
The Limcube version catches a lot though and is by no means a speedcube.
Limcube also produced a version with internal constraints on the Skewb moves, called WonderZ.
GB 3.5.1 - 24 + 2x2x2 - 48 Cube

 A 24 Cube crossed with a 2x2x2

PuzzleMaster6262 attempted one with his "Sand mech" [T] [T] generating some controversy... [T] [Y] [Y]

Cube4You shows a prototype made by James Li, called the Cadmium Cube (Cadmium is atomic numder 48): [Y]

Skewb+24

 A 24 Cube crossed with a Skewb - never attempted AFAIK.
GB 3.7.2 - Skewb + 24 + 2x2x2

 A triple cross - 24 Cube crossed with a Skewb and a 2x2x2.
Not made, but explored by Carl [T]
O2,O1 Hybrids
Each O2 puzzle can be combined with an O1 puzzle to make a (2,1) hybrid. O2's can also be combined with O2's to make even more complex hybrids. And of course O1's can be combined with O3's , etc. ad infinitum (in principle anyway). And let's not forget combining more than two types together in one puzzle! Yikes! Hybrids quickly get difficult to categorize, let alone to build. Also, without the clever use of magnets or detents, the resulting puzzles can be "squishy" - hard to hold without inadvertently moving something.

In the table below, the fundamental O1 cubes - the FT 2x2x2 and the VT Skewb - are represented in the rows. I have left out the row for the 24 Cube. The fundamental O2 cubes are represented in the five columns.

NOTE that an O1 combined with an O2 of the same turning regime simply gives an O3 of that type - I have outlined those four puzzles and they are already discussed above.

  FT 33 VT Mast. Skewb VT Dino VT Compy ET Heli
FT 23
FT O3 - Master / Revenge Cube
2x2x2 + Master Skewb = Hyper X
GB 3.4.2 - Super-X 		2x2x2 + Compy = ?  
Heli + 2x2x2
VT Skewb 3x3x3 + Skewb = ?  
VT O3 GB 3.2.3 - Elite Skewb
VT O3 GB 3.2.5 - Dino Skewb
VT O3 - Compy Skewb
Helicopter Skewb

Master Skewb + 2x2x2 - Hyper X - Gregoire Pfennig

 Master Skewb + 2x2x2 - Hyper X - Gregoire Pfennig [T] [S]
Dino + 2x2x2 - GB 3.4.2 - Super-X - Tom van der Zanden

 In Berlin, I got one of Tom van der Zanden's Super-X cubes [T] - the Super-X turns like a Dino plus a 2x2x2.

An early design by Wayne Johnson [T],
Realized as a full-custom design by Adam Cowan [T] [T]
Improved by Drew Cormier, who added magnets to stabilize it [T] [T] [Y]
Also made by jesseking from a Rainbow and keychain 2x2x2 [T]

Tom's version uses printed-in detents for stability, and having played with different versions, I would venture to say that Tom's is the best to date. Visit Tom's Shapeways shop.

Helicopter + 2x2x2

 Unbandaged Helicopter + 2x2x2 made by Eric Vergo in Jan 2011 [T]

Clay's Combo Copter [T]

Garrett Ong was working on one [T]

Also RubixFreakGreg [T] [S]

Kevin Uhrik sells a nice version of the Heli + 2x2x2 at his Etsy shop.

Helicopter + 2x2x2

 Combo Copter Plus by Braden, may be available at grigorusha's Etsy shop
Variations on the theme hybridizing an O1 Skewb with some sort of O2 Helicopter
Helicopter Skewb - Tom van der Zanden

 Helicopter Skewb - Tom van der Zanden [T] [S] also an unbandaged version [T] [S]

"namegoeswhere" also built one [T] [Y]

Skewby Copter Plus - Mf8

Skewby Copter Plus - Mf8

Skewby Copter Plus - Mf8
The Curvy Copter Plus (unbandaging cuts), plus Skewb
Has corners but no centers.
Morpho Aureola - FangShi Limcube

Morpho Aureola - FangShi Limcube

Morpho Aureola aka Curvy Copter Extreme from FangShi Limcube
The cuts that split the edges allow a partial helicopter turn to be cut by a skewb turn.
This has centers but no corners.
Twins Cube - Mf8

Twins Cube - Mf8

Twins Cube from Mf8
Mf8's answer to the Lim Morpho - Mf8 added the cuts that split the edges

SuperAntoniovivaldi posted a nice YouTube video comparing the Skewby Copter Plus, the Curvy Copter Extreme, and the Twins Cube.

Fission Skewb - Limcube

 Fission Skewb - designed by Guan Yang, produced by Limcube
Combines the Skewb with edge turns but the edge groups do not intersect. Note that although an edge group looks like it only consists of three pieces, the center "edge" piece is actually two pieces, so an edge turn affects four pieces.
Helicopter + Skewb + 2x2x2

[no image]

Helicopter + Skewb + 2x2x2
Higher Order Hybrids
Redi 3x3x3 - Eric Vergo

 Redi 3x3x3 - Eric Vergo
This puzzle turns at its vertices like Oskar van Deventer's Redi Cube, plus like a 3x3x3. Announced on the TwistyPuzzles forums, and available at Eric's Shapeways shop. Very clever, Eric!
Dreidel Cube
Dreidel Cube - an O2,O2 hybrid - designed by Guan Yang
issued by Lim Cube
Allows face turns like a traditional 3x3x3. In addition, the vertices turn along with the small pieces within the curved cuts surrounding them. A vertex can be turned 120 degrees but also 60 degrees - this aligns the diagonal cuts around the vertex with the normal 3x3x3 cuts and jumbles the small pieces.
Simple Dreidel Cube
Simple Dreidel Cube - an O2,O2 hybrid - designed by Guan Yang
issued by Lim Cube
The vertices turn along with the small pieces within the curved cuts surrounding them. A vertex can be turned 120 degrees but also 60 degrees - this aligns the diagonal cuts around the vertex with the normal 3x3x3 cuts and jumbles the small pieces. In this case, 3x3 face turns cannot be performed until the vertices are properly aligned.
Grilles Cube II

 Grilles II - Mf8
Lattice-X - Olz

 Lattice Cube with a 2x2x2 - a (4,1) hybrid. - a Super-X with the extra twisty tips of the Lattice Cube. Designed & made by Olz [T] [Y]
GB 3.6.1 - Dino + Helicopter - "Vestar"

 A Dino + Helicopter - aka Vestar
Compy + Curvy Copter = Flower Copter

Flower Copter Flower Copter Flower Copter

A Compy + Curvy Copter - Flower Copter designed by Minh Sanghsu and mass-produced by Lanlan
Butterflower Copter Cube - Lanlan

Butterflower Copter Cube - Lanlan Butterflower Copter Cube - Lanlan

Butterflower Copter Cube - Lanlan
A hybrid of a curvy copter, with a very shallow Compy (the edges involved in corner twists don't overlap).
GB 3.4.5 - Dino + 3x3x3 - Tom van der Zanden

 A Dino + 3x3x3 - made by Tom van der Zanden [W]
GB 3.4.7 - Master Skewb + 3x3x3 - Minh Shenghsu

 Master Skewb + 3x3x3 - Minh Shenghsu [T]
Ultra-X - Eric Vergo

 Eric Vergo's Ultra-X [T]
turns like a Rainbow Cube + 23 + small vertices
Geared
Gear Cube - Oskar van Deventer - Meffert

 Meffert has produced Oskar van Deventer's Caution Cube [S] and calls it the Gear Cube. The Gear Cube Extreme has four edge pieces in one layer replaced with alternatives that have less gearing. The Gear Cube Ultimate has alternative stickers requiring proper permutation of the small central gear pieces on each face.

Positions:
Gear Cube: 41,472
Gear Cube with edge base (small U piece) stickers: 165,888
Gear Cube Extreme: 2.56*1014
Gear Cube Ultimate (Extreme with edge base stickers): 3.28*1016

XXL Gear Cube

 XXL Gear Cube - a large twisty puzzle issued by Recent Toys. Thanks, Jaap!
Gear Barrel

 Gear Barrel - issued by Meffert
A shapemod of the geared 3x3x3
Gear Shift - Oskar van Deventer - Meffert

 Oskar's Gear Shift - Meffert
(black and white versions)
Video solution on Bram's YouTube channel
Geared Mixup Cube - Oskar van Deventer - Meffert

 Geared Mixup Cube - designed by Oskar van Deventer
produced by Meffert
A gift from Rox - thanks!
David's Gear Cube - Oskar van Deventer - Meffert

 David's Gear Cube - conceived by David Tzur (Alex Polonsky),
developed by Oskar van Deventer, issued by Meffert.
Gear Lucky Clover Heart Cube - LanLan

 Gear Lucky Clover Heart Cube - LanLan
Gear Skewb

 Gear Skewb - designed by Timur Evbatyrov
Produced by Calvin's Puzzle
Timur originally called it "Skewb des Soleils" [T] [Y]
based on his gear HMT
Circle / Crazy
Crazy 2x3x3 designed by Daqing Bao

 The Crazy 2x3x3 designed by Daqing Bao.
Genuine DaYan versions made by WitEden.
Available at Cube4you.
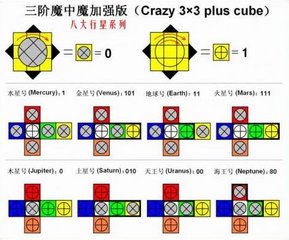
Crazy 3x3 Plus Cubes - DaYan

 The set of eight types of DaYan Crazy 3x3 Plus Cubes - "Eight Planets"
The circle pieces either do or don't turn with the face. The eight types are different ways of arranging dos and don'ts.
I got mine from Mefferts but you can find them at several vendors.
Super 3x3x4 - WitEden

 Witeden Super 3x3x4 black
Crazy 4x4 I - Mf8

 The Crazy 4x4 I from Mf8.

This cube was discussed on the Twistypuzzles forums in threads 14856 and 7918. You can see how this cube moves on YouTube here.

3.23*1053 positions

Crazy 4x4 II - Mf8

 The Crazy 4x4 II from Mf8.

3.1*1061 positions

Crazy 4x4 III - Mf8

 The Crazy 4x4 III from Mf8, purchased via Mefferts

3.1*1061 positions
Same as version II according to Jaap.

Cube and Cuboid Shapemods and Sticker Variations
Bump Floppy

 A "Bump Floppy"
YongJun Ghost Cube Irregular

 YongJun Ghost Cube Irregular
QJ Heart-to-Heart

 QJ Heart-to-Heart
A "dual-core" floppy.
Tonne

 The "Tonne" is a barrel form of the 2x2x2. It was produced in a few different color schemes. I bought one a while ago in Germany.
2x2x2 Shape Variations

Some 2x2x2 variations - Duff Beer can, Golden Syrup, Socube Rhinocerous, Lanlan Dodecahedron, the Trick Haus, 2x2x2 Bus, Hello Cube 2x2x2 Windmill, Yongjun House, Yongjun Elephant, Yongjun 2x2x2 Round, Yuxin 2x2 Magic Eye

2x2x2 Heads


Rubik's Crew Optimus Prime

2x2x2 Mad Hedz

As of late 2014, there is a new series of 2x2x2 head-shaped twisty puzzles, called Mad Hedz, issued by Intex Entertainment (aka New Entertainment).
I got four of the six from Amazon and two from Lightake.



Mad Hedz Black Breath and Mad Hedz Crazy Mummy

2x2x2 Star Wars figures

R2-D2 - Megahouse R2-D2 - Megahouse
R2-D2 - 2x2x2 twisty puzzle by Megahouse of Japan

BB-8 - Megahouse BB-8 - Megahouse
BB-8 - 2x2x2 twisty puzzle by Megahouse of Japan

Mental Flop (2x2x3 mod) - Grégoire Pfennig

 The Mental Flop by Grégoire Pfennig. [T] [S]
Visually, it's a cross between a 1x3x3 Floppy and Tony Fisher's Mental Block, hence the (great) name. Mechanically, it is isomorphic to a 2x2x3 (Slim Tower).
Shown in good company - with my original Floppy Cube hand-made by Okamoto, and my original Mental Block hand-made by Tony Fisher, along with a U.S. quarter.
Very stable and playable!
Fanxin Dinosaur Cube set (2x2x3)

 Fanxin Dinosaur Cube set
A commercially produced set of 2x2x3 shapemods.
Ultimate Cube

 Ultimate Cube
A commercially produced sticker variation. I have an original in its packaging.
Calendar Cube
4.4*1022 - Marvin Silbermintz

Rubik's Perpetual Calendar
(Kalender Kubus)
The "O" character on one
center has only 2
distinct orientations

Play with a virtual calendar cube here.

Rubik's Cube 4th Dimension
1.1*1022 - Erno Rubik

Rubik's Cube 4th Dimension
Four centers must have distinct orientations

Qubami - Kelvin Stott

 Qubami
Designed and produced by Kelvin Stott
The objective is to get 3 different colors and 3 different symbols on every row and column of every face.
Read about Qubami in the TwistyPuzzles forums.
Octagonal Prism
4.5*1017

Octagonal Prism
Jaap's page

Diamond Cube
2.0*106 = 2,425,500

Diamond Cube
Jaap's page

Truncated Corners 3x3x3 Cube

 Truncated Corners 3x3x3 Cube
2x2x2 Cuboctahedron

 The 2x2x2 Cuboctahedron (a truncated 2x2x2) - called the "Friki Cube" made by juanan [T]
3x3x3 Cuboctahedron

 The 3x3x3 Cuboctahedron
4x4x4 Master Cuboctahedron

 The 4x4x4 Master Cuboctahedron. Made by Jürgen Brandt, Sandy. [T]
5x5x5 Cuboctahedron

 The 5x5x5 Cuboctahedron. Made by Jürgen Brandt.
Jade Club Pillowed 3x3x3 Cube

 Jade Club Pillowed 3x3x3 Cube - Meffert
Venus Cube 3x3x3

 Venus Cube - a 3x3x3 shape variation with overlapping - designed by Evgeniy Grigoriev (he called it the "Fluffy Cube") - produced by Meffert
Pandora Cube 3x3x3

 Pandora Cube - a 3x3x3 variant by Moyu
Phoenix Cube (Bai Niao Chao Feng) - Shengshou

Phoenix Cube - Shengshou Phoenix Cube - Shengshou Phoenix Cube - Shengshou Phoenix Cube - Shengshou

Phoenix Cube aka Bai Niao Chao Feng - Shengshou
A Fisher Cube variant.
Similar to the "Copter Tower" and also the "Turtle Cube" both by Troy Robinson (rcpongo). [Y]
Can be solved using the Sledgehammer (R'LRL').

The Brain Cube, designed by Jason Freeny. A 3x3x3 clad with a squishy material called Kraton, and textured to resemble a brain. Solve by aligning all the fissures. Comes in a glass jar, formaldehyde not included.
Purchased from Marbles The Brain Store.

King Pillow Cube - 3x3x3

 King Pillow Cube
A commercially produced shape variation.
Confused Pillow Cube - 3x3x3

 Confused Pillow cube from "Socube"
Hexagonal Prism 3x3x3

 Hexagonal Prism 3x3x3
Rhombohedron 3x3x3

 Rhombohedron 3x3x3
Truncated Hexagonal Dipyramid 3x3x3

 A "Blue Diamond" (Truncated Hexagonal Dipyramid shape mod to a 3x3x3).
These are being mass-produced in China.
Hexagonal Dipyramid 3x3x3


 A cheap way to make a Hexagonal Dipyramid - combine the parts from two Guo Jia diamonds.

Now Hexagonal Dipyramids are mass-produced by Dian Sheng.
3x3x3 core

Hexagonal Dipyramid 4x4x4

 Super Dipyramid
(hexagonal dipyramid from 4x4x4 core)
Dian Sheng "Tank Diamond"

 Dian Sheng "Tank Diamond"
Dian Sheng Pyramid (aka "aXe")

 Dian Sheng Pyramid (aka "aXe")
designed by John Lin
Various 3x3x3 Shape Variants


Various 3x3x3 Shape variants, including: Heart, Apple, Star, Egg/Potato, Cake, Concave Cube, Ingots (3 colors), Carni Chaak head, FangShi Limcube Deformed Centrosphere, Egg Pig

Various 3x3x3 Sticker Variants, Color Variants, and Size Variants
Extended and Multicore Cubes
3x3x3 Extended to 3x3x4

 3x3x4 Extended Cube
This simple extended cube-variant has an extra piece glued to each of the nine facelets of one face.
3x3x3 Extended to 3x3x5

 3x3x5 Extended Cube
This simple extended cube-variant has an extra piece glued to each of the nine facelets of two opposite faces.
3x3x3 Extended to 4x4x4

 3x3x3 Extended to 4x4x4
This is a cheap and simple extended cube-variant from Hong Kong, not a 4x4x4 Evil Twin as the description led me to believe. Caveat Emptor!
Extended 3x3x3 with Deleted Corners

 An Extended Cube.
Mini Evil Twin - Mike Grimsley

 Mini Evil Twin
Made by Mike Grimsley.
Siamese Cube chains

 Double and Triple Cubes
Available commercially from various sources, made from keychain 2x2x2 cubes. Two cores share a corner in "Siamese" configuration.
Bandaged and Otherwise Constrained
Bandaged Cube - Meffert
1.0*106 = 1,108,800

Bandaged Cube
Jaap's page
Andreas Nortmann has investigated bandaged cube variations - Andreas says there are 7356 different bandaged 3x3x3 cubes, of which 5705 are (subjectively) non-trivial. Read his articles in the TwistyPuzzles forum: [T] [T] [T] [T] [T] ; also Hidetoshi [T]

Bandaged Cube Kit - Cubetwist

 A Cubetwist Bandaged Cube Kit, ordered from Lightake
Nightmare Cube - Tanner Frisby

 Nightmare Cube from Tanner Frisby [T] [Y] [Y]

A Nightmare Cube is a bandaged 3x3x3 hidden inside a 2x2x2 shell.

Before the first move, all normal 2x2x2 twists are permitted. After a few turns, however, the bandaging comes into play so various moves become blocked, and then solving becomes a nightmare! Tanner told me the YBR corner has no bandaging.

In October 2008, Adam Cowan issued free STL files for the Nightmare Cube, in the TP Forums, based on an idea mentioned by Noah Hevey in a post from March 2008. Tanner's version is made from a different core, though.

TP Forum member "sublime" made one from wooden corner pieces and a modified keychain 3x3x3 core, and then posted about his copy of the printed version.

Also see: [T] [T]

Folks have noted that solving a Nightmare cube is more akin to navigating a hidden maze, than applying conventional operators. The solution methodology is discussed at Jaap's page.

New Spring 2x2x2 Cube with Bandaged 3x3x3 Core

 A "New Spring" clear 2x2x2 with internal colored bandaged 3x3x3
The New Spring version is not a "Nightmare" cube, since all 2x2x2 moves always work. But restoring the internal 3x3x3 is not trivial!
Various other Bandaged Cubes

 Just FYI, there are a slew of other bandaged cubes available, including 4x4x4 cubes.
Camouflage Cube 3x3x3 - WitEden

 Camouflage Cube
A bandaged and extended 4x4x4
Ordered from WitEden
Various versions are available.
Bermuda Cube - DaYan

 DaYan Bermuda Cube Neptune (black)
One of a series of eight types.
Latch Cube - Okamoto

 Latch Cube - Okamoto
Quarter Cube - Okamoto

 The Quarter Cube, designed by Katsuhiko Okamoto and Takafumi Haseda, produced by Chronos Co. Ltd.
Constrained Cube - Tom van der Zanden

 The Constrained Cube designed by Tom van der Zanden. Several versions available that have different side turning constraints (90,180,270, and Ultimate). I ordered the "Ultimate" version.
Pocket Cube - Justin Eplett - Meffert
Pocket Cube - designed by Justin Eplett,
produced by Meffert.
A 3x3x3 with clever bandaging and extensions. Two different color schemes.
Axised Cubes
If the standard 33 cube is rotated 45° about one face's axis (e.g. z axis) then built up and cut down to be re-formed into a cube, one obtains the Fisher's Cube; approx. 30° around z [T] gives the Windmill Cube; 45° around z and x (or 90° about an edge-to-edge axis) gives the Slice Cube; combining Fisher's and Windmill gives a "normal-sized" Greenhill's Cube (which is actually larger - Anthony says [T] it is "a 'Truncated Cube' (corners trimmed down to triangles), stood on one corner then built out to a Cube shape. This basically determined the edge length - 77mm."); 60° about a corner-to-corner axis gives the Axis Cube [T] [T]. An "axised" Cube with twists, reformed into a cube gives the Ghost Cube [T].

Fisher's Cube

 Fisher's Cube - originally designed by Tony Fisher, now mass-produced
An axis-rotated 3x3x3 (single axis x 45 degrees)
Solve as a 3x3x3, but also has four of six face centers that can be rotated by 90, 180, or 270 degrees.

These are the Supercube face algorithms - algorithms exist to rotate a single face center by 180, or a pair - one by 90 and another -90.

U180: ( (U R L U2) R' L') x2

U90 & F-90: F B' L R' - U D' F' U' D - L' R F' B U

U90 & D-90: R L' F2 B2 R L' U R L' F2 B2 R L' D'

Master Fisher Cube - Moyu

 Moyu Master Fisher Cube
Fisher's Cube / Diagonal Cube - 8-color sticker variant

 Fisher's Cube / Diagonal Cube
8-color sticker variant
Windmill Cube


 Windmill Cube
Also, stickerless version.
Slice Cube

 At the 2012 New York Puzzle Party (NYPP) hosted by Tom Cutrofello, I bought this hand-made Slice Cube from fellow attendee and twisty puzzle enthusiast "Zhewei." He had posted about this puzzle on the Twisty Forums here.
Axis Cube

 Axis Cube
Designed by Adam Cowan, made (hand-cast) by Frank Schwartz (RIP).

Now mass-produced.

Moyu Aosu Axis 4x4

 Moyu Aosu Axis 4x4 (blue)
Ghost Cube

 Ghost Cube
Designed and made (hand-cast) by Adam Cowan and Jason Smith.
Purchased from Jason Smith.
Possibly the most difficult of the "axised" designs.
Ghost Cube - Meffert

 Meffert has mass-produced the Ghost Cube
I got examples in purple metallic, and black with white stickers.
Yong Jun (YJ) Moyu Crazy Yileng Fisher Cube

 Yong Jun (YJ) Moyu Crazy Yileng Fisher Cube - another "axised" 3x3x3
Pitcher Insanity Cube - Calvin's Puzzles

 Insanity Cube - designed by David Pitcher [T],
issued by Calvin's Puzzles
DaYan Tangram Cube

 DaYan Tangram Cube
Isomorphic to the DaYan Pentahedron 3x3, but with super centers.
Skewb Shapemods
Skewb X-treme

 Skewb X-treme - 10-color version, designed by Tony Fisher,
produced by Meffert.
Golden Cube - Tony Fisher

 Meffert's Fisher's Golden Cube
Perhaps the most famous of the Skewb mods, produced commercially by Meffert.
I bought the "Lunar New Year" set of three, and also a black one.
Mental Block - Tony Fisher

 Tony Fisher's Mental Block aka Rubik's Layer
Custom-made by and purchased from Tony. A buildup of a full-sized Skewb using add-on prosthetics. First made by hand by Tony back in 1996. [W]
Curvy Rhombohedron Skewb - John Lin

 Curvy Rhombohedron Skewb - designed by John Lin
Squished Skewb - John Lin

 Squished Skewb - designed by John Lin
This is pretty large, and a very nice turning puzzle!
QiYi Mofangge Twisty Skewb

 QiYi Mofangge Twisty Skewb
Skewb to Cuboctahedron - Maruyama

 A Skewb with 3D printed prosthetics, modded into a Cuboctahedron.
Purchased 1/2018 from "Maruyama" of Japan. [Y]
Edgematching
Einstein Cube
12^6 = 2,985,984 (Einstein w/ 12 pos./face)
3*106
24^6 = 191,102,976 (Turn 12)
1.9*108

Einstein Cube
A faces-only cube (granted, the faces are rounded).
This type of 3D edgematching puzzle is included here because I consider them "faces-only" versions of twisty polyhedra - no corners and no edges.
12 positions per face. A similar puzzle called "Turn Twelve" has 24 positions per face.

Cuboids

This chart is a 3-D scatter plot showing fully functional cuboid puzzles that have been made either commercially or as custom creations. A cuboid has a cubic or brick shape, with dimensions k x m x n. "Fully functional" cuboids allow turns through every cut - "extended" and multi-core (e.g. chaos, evil-twin, fused, and siamese) cuboids are not included here.

The puzzles in the chart are positioned such that k <= m <= n. In the chart, the left-to-right (x) axis is k, the front-to-back (y) axis is m, and the bottom-to-top (z) axis is n. Each axis except m (y) runs from 1 to 7 - puzzles where a dimension exceeds 7 are few and are shown off the chart. I omitted m=1 to reduce clutter. This prevents the inclusion of the so-called 1x1x1 (no big loss IMHO), and forces the 1x1x2 to be located at 1x2x1, the only violation of the m<=n rule. 1.1.n for n!=2 are omitted. A red "post" beneath each item gives a hint as to z scale.

In the table below, mass-produced commercially available puzzles are highlighted like this. Cuboids I have are highlighted like this. Cuboids I don't have and would like to see mass-produced are highlighted like this.

When available, links are given to YouTube videos (shown as [Y]), websites (shown as [W]), TwistyPuzzles forum threads (shown as [T]), and Shapeways (shown as [S]).

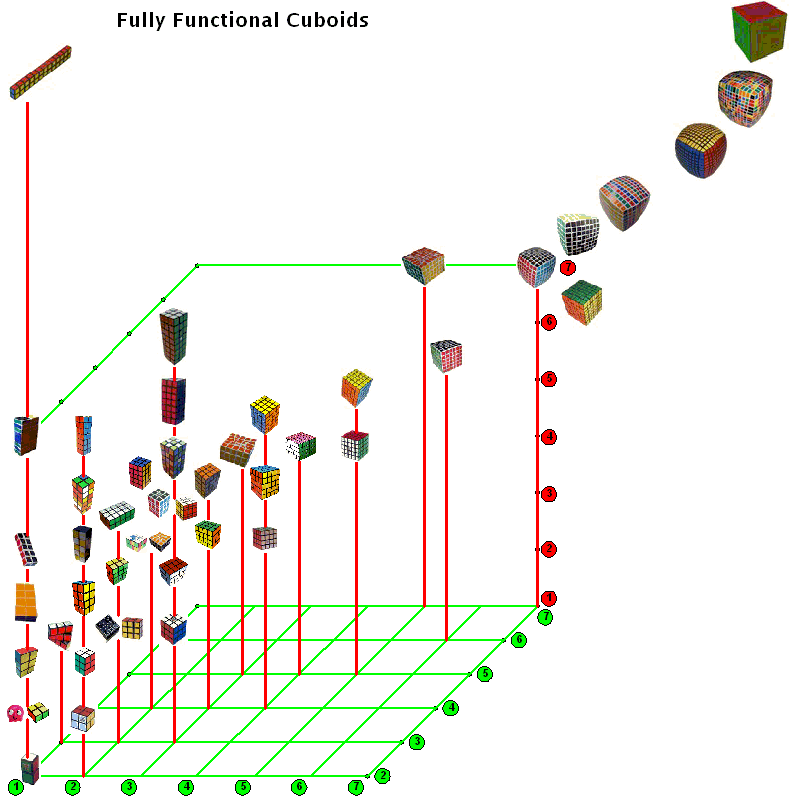
Kevin Sadler has posted a nice overview of cuboid puzzles on his "Puzzlemad" blog. Kevin specifies subcategories for the cuboids:
  • Domino Cuboids - of the form N.N.(N+O) or N.(N+O).(N+O) where O is odd. No shapeshifting - oblong sides only turn 180°.
    e.g. 1.1.2, 1.2.2, 1.2.4, 1.4.4, 2.2.3, 2.3.3, 2.3.5, 2.5.5, 3.3.4, 3.4.4, 4.4.5, 4.5.5, etc.

  • Shapeshifting Cuboids - of the form N.N.(N+E) where E is even, N > 1.
    e.g. 2.2.4, 3.3.5, 4.4.6, etc.

  • Brick Cuboids - N.(N+O).(N+E) or N.(N+O).(N+O+2) - shapeshifts in only 2 of 3 axes.
    e.g. 1.2.3, 2.3.4, 3.4.5, etc.

  • Floppy Cuboids - N.(N+E).(N+E)
    e.g. 1.3.3, 2.4.4, 2.4.6, 3.5.5, 3.5.7, etc.
    The 3.5.7 shares characteristics of the Brick and Floppy classes.

Joshua Bell has a nice photo of his cuboid collection on Flickr. And in the TP Collecting forum: [T]

Table last updated Jan. 18 2022.

The 1.?.? puzzles:

  • 1.1.1 - Only for completists (but are you sure you have the correct colors? :-)
  • 1.1.2 - custom made by many - e.g [T]

  • 1.1.3 - You can buy a memory stick clothed in a 1.1.3 puzzle from various places, but only one cubie moves. Rubik's now offers an LED flashlight 1.1.3.

  • 1.1.4 - avail from hknowstore
  • I'm not tracking other 1.1.n...
  • 1.2.2 and the Morph - VeryWetPaint has a 4-piece design he calls the Minimis [T] [S]; hollow version by "mu puzzles" [T] [W]

  • 1.2.3 - Scott Bedard ; micro version by "mu puzzles" [T] ; drew11 (Andrew Kirfman) [T] [Y] [S] ; floppy version (shapeshifting) by drew11 [T] [S] ; inverted version by will_57 [T] [T] [Y] [S] ; Babyface version (1x2 and 2x3 faces, not 1x3) by DARKYtheCUBER [T] [Y] ; mass-produced Rubik's Junior Bear - based on the Ozo Bear by TP member "Sain" (Emmanuel Carrillo) [T] ; mass-produced Qboid by Brainwright - designed by David Pitcher [T]

  • 1.2.4 - Steryne (Tanner Frisby) and "caveman999" [T] [Y] [Y] also free STLs from Olz [T]; "kequals" [Reddit] [Thingiverse] [Imgur]

  • 1.2.5 - Olz (Ola Jansson) [W] [T] [Y] [Y] (version 1.5) [W]; hollow version by "mu puzzles" [T] [W]; mass produced by IQube in Japan [W]
  • 1.2.6 - "kequals" [Reddit] [Thingiverse] [Imgur]
  • 1.2.7 - Alex Ozer (Mindstormscreator) [Y] [Y] [T] ; drew11 [T] [Y] [S] ; clauswe (?) [T]
  • 1.2.8 - not yet made
  • 1.2.9 - Murilo Semeghini [T]; mass-prod. by Meffert [T]
  • 1.2.11 - clauswe (?) [T]
  • 1.2.13 - Oskar van Deventer's "Unlucky Twist" [Y]
  • 1.2.111 - Greg [T] [Y]
  • 1.3.3 Floppy Cube designed by Okamoto. His Scramble Cube enhances the mechanism and allows further twists.

  • 1.3.4 - Designed by Olz (Ola Jansson) and built by "incredible" (Karl-Heinz Diekmann) [T] [Y]; also made by Tanner Frisby [T]

  • 1.3.5 - Designed by "Door" (Mark Segedin), made by Karl-Heinz Diekmann [T]; also Olz [T]; Claus Wenicker [T] [Y]; Traiphum [T]
  • 1.3.6 - Mark Segedin (Door) [T]
  • 1.3.7 - David Marcos (180 degree turns only) [T]
  • 1.3.9 - zse [T]
  • 1.4.4 - Designed by Olz and attempted by "elijah" but not completed [T]; completed by Karl-Heinz Diekmann [T] [T] [Y] ; also, "Confusion" made one from a bandaged/extended 4.6.6 block [T];
  • 1.4.5 - Door (Mark) [T] [Y];
  • 1.4.6 - Greg, for Claus Wenicker; zsé [T]
  • 1.4.7 - Door (Mark) [T] [Y];
  • 1.5.5 - Designed by Murilo Semeghini [T] [S]; Traiphum [T]; Sam Jiang [T]
  • 1.5.6 - Mark (Door) [T]
  • 1.5.7 - zse [T]

  • 1.6.6 - Greg [T] [Y]
  • 1.7.7 - grigorusha [T]
  • 1.8.8 - Greg [T]
  • 1.9.9 - "yummyyummypbj" (Matt Bahner) [T] [Y]
  • 1.11.11 - Greg's Flopsanity [T]
The 2.?.? puzzles:

  • 2.2.2 - commercially produced by Rubik (e.g. the Pocket Cube), Eastsheen, and others

  • 2.2.2.2 - Melinda Green - "the world's first" 3D analogue of a 4D 2x2x2 [T] [Y] [W]

  • 2.2.3 - at first custom mods - e.g. Jin Kim, Tony Fisher, then commercially produced by Gentosha based on Okamoto's Slim Tower design

  • 2.2.4 - Tony Fisher 2003 based on a Revenge core [W] [Y], by Garrett Ong [T] [S], then commercially produced by Mega-House based on Hidetoshi Takeji's design [T]

  • 2.2.5 - Jesse Werner [T] [T] [Y], Kickflip1993 ; clauswe (?) [T]; Offset center version Mass-produced by WitEden

  • 2.2.6 - Tony Fisher [W]; Jesse Werner [T]; Karl-Heinz Diekmann, based on design by Ola Jansson [T]; Mass-produced by WitEden

  • 2.2.7 - Tony Fisher [W] [Y]; Mass-produced by WitEden [T]
  • 2.2.8 - Ola Jansson [T]
  • 2.2.9 - Ola Jansson [T] [Y]
  • 2.2.10 - "yummyyummypbj" (Matt Bahner) [T] [Y]
  • 2.2.11 - Greg [T]
  • 2.2.12 - Greg
  • 2.2.13 - Greg
  • 2.2.14 - Greg [T]

  • 2.2.23 - Oskar's "Overlap Cube" [T] [Y] [S]
  • 2.3.3 - the Domino first produced by Rubik, now available from Asia ; also a "split" version (each edge piece split in half) by Chino [T]

  • 2.3.4 - Okamoto's Step Up Tower, Tony Fisher [W] [Y], "Marco768" [Y], Garret Ong [T] [T] [Y] [S] , Tanner Frisby [Y] [Y] , now mass-prod. by Mf8

  • 2.3.5 - "chris the cynic" (Chris Whitham) [T] [Y], Designed by Ola Jansson, built by Clay & Eva [Y] [Y] , Traiphum [T] [Y], new version [T], MattStudiosPuzzles on Etsy.

  • 2.3.6 - made by door and clauswe [T] [Y] ; A multi-core chaos-type "Monolith" was made by Italrubik (Fabio) [T]
  • 2.3.7 - Designed by Ola Jansson, built by Clay & Eva [T] [Y]; Traiphum [T]
  • 2.4.4 - the Rylox Prism by Mark Longridge [W] [T]; versions by Olz [Y] [T] [S] Solve video: [Y] v3.25 [T] ; Tanner Frisby [T]; WitEden mass-produced their "Camouflage Cube 2x4x4" which is not quite fully functional [W]

  • 2.4.5 - made by Muffet (Matthew Ray) and clauswe [T] [Y]; Traiphum [T]; Tony Fisher made the multi-core Cubie Chaos 1 [W]

  • 2.4.6 - Greg [T]; Hunter Palshook [T]; A multi-core chaos-type version Stonehenge was made by Italrubik [T]; Hunter Palshook's version mass produced by Calvin's Puzzle

  • 2.4.7 - not yet made
  • 2.5.5 - Ola Jansson [T] ; made by elijah [T] [Y]; made by Karl-Heinz Diekmann [T] [Y] ; muffet [T] [Y]; Traiphum [T]
  • 2.5.6 - Claus Wenicker, from a 6x6x6
  • 2.5.7 - Traiphum [T]
  • 2.6.6 - Greg [T]; Traiphum (FB)
  • 2.6.7 - Traiphum [T] posted 12/24/21
  • 2.6.10 - gr_cubed (Liapis Nikolaos) [T]
  • 2.7.7 - Traiphum (FB) [Y]
  • 2.8.8 - Traiphum [T]
The 3.?.? puzzles:

  • 3.3.3 - the twisty that started it all

  • 3.3.4 - Okamoto's Phantom Cube, Jin Kim [W], TomZ posted free STL files [T], then offered commercially by James Lee [W]; cubic version by "MaCheezm0" (prop. 3x3x4 with thin top & bottom layers) [T]

  • 3.3.5 - done in three styles - proportional, cubic, and "Lazy Man's" -
    • Proportional versions include Okamoto's Grown Tower, Tony Fisher [Y] [W], Jin Kim [Y] [W], Olz [T] [Y] [W], Smaz [T] [W]; guoguo [T]; RyanZ [T] ; Sigurd [T] ; Calvin & Evgeniy [T] - mass-produced by Calvin [W]
    • The cubic version was first made by Adam Cowan and Jason Smith [T], then offered commercially by James Lee [W]
    • The "Lazy Man's 3x3x5" was made by "guoguo" [T]

  • 3.3.6 - Traiphum [T] [T] [Y]; non-proportional version from Witeden [T]; proportional by CBCubes [T] [Y] ; proportional off-center version mass-produced by Witeden

  • 3.3.7 - Traiphum [T] [Y]; Sigurd [T] [Y];
    • Cube4You cubic;
    • Witeden proportional

  • 3.3.8 - Traiphum [T] [Y]; WitEden [W]
  • 3.3.9 - Traiphum [T] [Y]; "Thien" says he's working on one [T]; cubic version by WitEden [T] [Y]
  • 3.3.10 - Greg & Claus (proportional, not pillowed) [T] [Y] ; Traiphum (pillowed) [T]
  • 3.3.11 - Greg & Claus (proportional, not pillowed) [T] [Y]
  • 3.3.12 - simple truncation of Greg's 3.3.14, by Claus [T]
  • 3.3.14 - Greg & Claus [T] [Y]
  • 3.4.4 - Okamoto's Specter Cube, Jin Kim [W] [T] (sold in March 2008 for over $660), Tony Fisher [W], Tanner [T] [T] [Y], Traiphum [Y], Garrett Ong [T] [Y] [S]; "blackout" (pillowed) [T]; "Dankeeen" (pillowed) [T] [Y]; Aleh [T]; Ayi's version is mass-produced [Y]

  • 3.4.5 - TomZ (Tom van der Zanden) [S] [T] [Y] [T] [T] [T] [Y] [S]; Traiphum [T] ; produced commercially by Mf8
  • 3.4.6 - "Olz'ed" version designed by "Door" (Mark), made by Karl-Heinz Diekmann [T]; proportional version by Greg and Claus [T]
  • 3.4.7 - proportional by Greg, for Claus Wenicker; A multi-core chaos-type was made by Italrubik [T] ; another multi-core by ENCuber [T]
  • 3.5.5 - Olz [T] [Y] [Y]; Olz's proportional version [T] ; Eitan's cubic 3.5.5 (CAD/3D/cast) [T] [Y]; Murilo Semeghini [S]; Traiphum [T] [Y]; Hunter Palshook [W]; TallPawn (Floyd Newberry) [T]
  • 3.5.6 - Greg [T] [Y]
  • 3.5.7 - "The Ultimate Shapeshifting Cuboid" (can shapeshift in all directions) - bulbous version, designed by Nkrasn11 [T] [T] [Y] - built by clauswe [T] [Y]; brick-shaped version designed by Greg, made by "drwho" [T] [S] [Y]; Hunter Palshook [T]; Ian c [T]; Traiphum
  • 3.6.6 - Greg [T]
  • 3.6.7 - Traiphum [T] posted 12/24/21
  • 3.6.8 - Claus Wenicker, from a stickerless 8x8x8
  • 3.6.9 - Greg [T]
  • 3.7.7 - Greg [T] [Y]; Traiphum (shown on Kevin's blog: [W]); Jhon's mods [F]
  • 3.7.11 - Liapis Nikolaos [T]
Everything else:

  • 4.4.4 - Rubik's Revenge (Peter Sebesteny), also Eastsheen A4

  • 4.4.5 - Tony Fisher [W] [Y], Aleh Hladzilin [T] [T], Zamora [T], Thomas [T], Jin Kim [W] [Y] [T] [T], "p|astic" [Y] [T] [T] [T], Tanner Frisby [Y] [Y] [Y], Garrett Ong [T] [T] [Y] [T], Ayi's 4x4x5 [T] [W]; cubic 4x4x5 Garrett [Y]; Chino's cubic 4x4x5 [T] [Y]

  • 4.4.6 - Tony Fisher [W] [Y]; "open-source" version commissioned by Joshua Bell and designed by TomZ [T] [Y] [S] ; mass-prod. by "Calvin's Puzzle" [T]
  • 4.4.7 - Door (Mark) & clauswe [T] [Y]
  • 4.4.8 - Greg [T] [Y]
  • 4.4.9 - Greg [T]

  • 4.5.5 - Aleh (Oleg) (using 3 Eastsheen A4 cubes) [T] [T], Tanner Frisby [T] [T]; Ayi's 5x5x4 [T] [W] [Y]

  • 4.5.6 - Tom van der Zanden [T] [Y] [S] [W]
  • 4.5.7 - Traiphum [T]
  • 4.6.6 - Clauswe [Y]; Dan [T]
  • 4.6.7 - Claus Wenicker, from an 8x8x8; Traiphum [T] posted 12/24/21; made as Evil Twin multi-core type, by "chris_joe" back in 2007 [T]
  • 4.6.8 - "Jerm" Jeremy Isenburg [T] [Y]
  • 4.7.7 - Traiphum [T] [Y]
  • 4.8.8 - "63falcondude" (Matt Hand) [T] [Y]
  • 5.5.5 - The Professor or Wahn, also Eastsheen A5, and Verdes V-5
  • 5.5.6 - Tony Fisher [W] [T] [Y]
  • 5.5.7 - Designed by Ola Jansson, made by Karl-Heinz Diekmann [T] [T]
  • 5.5.8 - by Greg [T]
  • 5.5.9 - by Greg [T]
  • 5.6.6 - first claimed by Ilya Toporgilka 2016 [T]; Traiphum in 2018 [T][Y]
  • 5.6.7 - "cube_master" on the Mf8 BBS [T]; Gregoire Pfennig [T]; Dr. Who [S]; Chaos version by Felixouchon [Y]
  • 5.7.7 - Olz [T] [Y] [Y]; clauswe sanded down a V-Cube 7x7x7 [T] ; Traiphum (shown on Kevin's blog: [W])
  • 5.7.9 - Greg [T] ; Traiphum [Y]
  • 5.9.9 - Ralph Viggiani [T]; Traiphum [T]
  • 6.6.6 - the V-6 by Verdes [W]; other designs by Wayne, Laurent Blanc [W], discussed back in 2005 [T]
  • 6.6.7 - Tom van der Zanden [T] [Y]
  • 6.6.8 - designed by Jeremy Isenburg for crazybadcuber (Dan Fast) [T] [S] [Y]
  • 6.7.7 - Greg [T] [Y]
  • 6.7.8 - thechincheachilla / Reiden Chea [T] [Y] [Etsy]
  • 6.8.8 - Traiphum [T]
  • 6.8.10 - Jeremy Isenburg [T] [Y] [S]; Traiphum [T]
  • 7.7.7 - the V-7 by Verdes [W] (discussed earlier); Tony Fisher's cubic 7x7x7 [W] [T], also Etienne de Foras [W]; another proportional 7.7.7 by "jeff79511" of Taiwan [Y] [W] (there is some controversy as to whether it's a hoax) [T] [T]
  • 7.7.9 - Liapis Nikolaos [T]; "geomancam" using 3D printed extensions on a 9x9x9 [T]
  • 7.9.9 - Traiphum [T]
  • 7.9.11 - "TwistyTex" Casey Weaver [FB]; Traiphum [T]
  • 8.8.8 - ShengShou (about $66), Yuxin; the DaYan 8x8x8, a mod by Daqing Bao [T] [Speedsolving.com forum]; sky and danny (Daniel Baamonde) [T] [Y]
  • 8.10.10 - Traiphum [T]
  • 9.9.9 - ShengShou (about $80), Yuxin
  • 10.10.10 - ShengShou (about $120), Yuxin; Greg [T] [T] [Y]; (from Mf8 BBS) [T]
  • 11.11.11 - Shengshou, Yu Xin (about $130); Tobey; ZhiSheng; a one-off custom mod made by Tony Fisher and un-named friends - [T] [W]
  • 12.12.12 - Leslie Le's "The Twelfth Cube" [T] [T] [T] ; Greg [T] ; mass-prod by Shengshou, Moyu (about $150) [T]
  • 13.13.13 - Yong Jun [T]; MoYu (about $250-300); ShengShou
  • 14.14.14 - mass-prod by Shengshou (about $250)
  • 15.15.15 - Moyu (about $380-450)
  • 16.16.16 - mass-prod by Shengshou 2021 (about $356)
  • 17.17.17 - YuXin (about $600-750; $700 on Amazon Jan 2018); Oskar van Deventer's 17x17x17 design he calls "Over the Top" [S]; a build was attempted by "clauswe" but the result isn't truly usable [T]. Oskar's functional version 3 was announced at the NYPP2011 [T]
  • 19.19.19 - Shengshou, $899 Sep 2020
  • 21.21.21 - Moyu, $1500 Oct. 2021
  • 22.22.22 - article on ruwix.com
  • 25.25.25 - TP forum member "HoleCubes88" 1/14/22 [T] [Y]
  • 33.33.33 - Greg Pfennig [Y]

 

Another way to organize the cuboids is by cross-section versus number of layers,
though this format contains redundant information.
Also, a few puzzles (most not yet made) are omitted as I have compressed the table.
The table below summarizes which have been mass-produced, custom-made, and not yet made.
P means proportional. C means cubic. N means non-proportional.
The heavy squares outline square cross-sections and cubes. Asterisks indicate puzzles I have.

cross-sec. =>
layers 		2x1 2x2 2x3 2x4 3x1 3x3 3x4 3x5 3x6 4x4 4x5 5x5 5x6 6x6 7x7
1   * *   * * *     *   *      
2 * * * * * * *     *   *   *  
3 * * * * * * * * P C *   P N * * * *      
4   * * * * * * *   * * *      
5 *         * P C * * *   * * *      
6       *     P N *       *       *  
7             P * C *   *             *
8                              
9             P C *                  

 

The table below focuses on cuboids I have obtained. There are many other examples I don't have - for information about them, see the tables above.

Cuboids - 1-Layer
Rubik's LED Flashlight 1x1x3

 1x1x3
Rubik's LED Flashlight 1x1x3
1x1x4

 1x1x4
The Morph, 1x2x2

 1x2x2
The Morph, and a black cuboid
Only 6 positions possible!
I find this harder to mix up than to solve.
1x2x3

 1x2x3
by Scott Bedard.
Qboid 1x2x3

 1x2x3
Qboid - designed by David Pitcher [T]
Issued by Brainwright
Rubik's Junior Bear 1x2x3

 1x2x3
Rubik's Junior Bear
The Ozo bear - designed by Emmanuel Carrillo [W] [T] has been licensed and mass-produced by Rubik.
The original facial features are simplified.

The 1x2x3 Bear was followed by the 1x2x3 Cat, Dog, and Bunny.

IQube 1x2x5

 1x2x5
IQube blue - www.hanayamatoys.co.jp
and IQube red - www.hanayamatoys.co.jp
Pocky 1x2x5

Pocky 1x2x5 Pocky 1x2x5 Pocky 1x2x5

1x2x5
Pocky 1x2x5
Jade Chopsticks 1x2x9

 1x2x9
The Jade Chopsticks, a 1x2x9. [T] The ambigram on it was designed by John Langdon.
Based on the 1x2x13 designed by Oskar van Deventer and the 1x2x9 designed by Ola Jansson.
Mass-produced by Meffert.
Floppy Cube 1x3x3 - Okamoto (custom)
Floppy Cube 1x3x3 - Gentosha (mass prod.)

 1x3x3
Floppy Cube - Katsuhiko Okamoto
I have an original custom-made by Okamoto, and the commercial version now available from Gentosha.
This won First Prize at the IPP26 Design Competition. At the time, it was a revelation on how to build a 1-layer puzzle and yet keep the corners attached.
Scramble Cube 1x3x3

 1x3x3
3,041,280 positions

The Scramble Cube - Katsuhiko Okamoto
Okamoto's follow-up to his Floppy Cube -
originally known as the Super Floppy when it won the Puzzle of the Year award in the 2009 IPP Puzzle Design Competition. Knock-offs were promptly produced but did not function in the same way - the Scramble Cube does not allow naked edge centers to be rotated.

1x3x4

 1x3x4
Designed by Ola Jansson, made by Tanner Frisby
1x4x4

 1x4x4
Designed by Ola Jansson, made by Karl-Heinz Diekmann
One of my favorite twisties!
1x5x5

 1x5x5
designed by Murilo Purcineli Semeghini ("mu puzzles" on TP) [W]
Purchased from his Shapeways shop (defunct).
A version with a different look, based on Ayi Liu's 4x5x5, was made by Traiphum [T]
Cuboids - 2-Layer
2x2x2

 2x2x2
[See main Hexahedral section]
Slim Tower 2x2x3 (custom)
Slim Tower 2x2x3 - Gentosha (mass prod.)

 2x2x3
241,920 positions.

- this mod is known as the "Slim Tower." I got a hand-made version a while ago but I forget from whom. Katsuhiko Okamoto's version is now commercially available from Gentosha.

Solution Algorithms:

1) Gather top 2x2 face
2) Solve top face - swap adj. UFL + UFR:   F U' F U F  R U R U' R
 (Do twice for a diag. swap.)
3) Flip & solve the other 2x2 face as top

4) If not done, solve the middle layer - 0, 1, or 2 will be correct...
  M is middle layer CW seen from top

4a) if 0, do   R M2 R  (FL<->FR + BL<->BR)
  if not done, do 4b or 4c

4b) if 1 (at BL) -

  CW 3-cycle:   M' R M R

  CCW 3-cyc:   R M' R M  (inverse of above)

4c) if 2:

  swap adj. FR + BR:  (R U2)3

  swap diag. FL + BR:  F (R U2)3 F  (F converts to adj. swap)

(See Robert Munafo's site.)
2x2x4 - Garrett Ong (custom)
2x2x4 - Hidetoshi Takeji - Rubik (mass prod.)

 2x2x4
I bought one of Garrett Ong's hand-made 2x2x4 puzzles (before I knew they'd be mass-produced). Later, I received a copy of the new Rubik's 2x2x4, signed by designer Hidetoshi Takeji.
2x2x5

 2x2x5
2x2x5 - WitEden (offset center)
2x2x6

 2x2x6
2x2x6 - WitEden
A beautiful, hefty, fully functional puzzle.
2x2x7

 2x2x7
2x2x7 - WitEden
Domino 2x3x3




 2x3x3
4.0*108

Rubik's Domino - Erno Rubik

This is available both vintage and new in various versions. The most common vintage version is known as a Groove Domino (its internal mechanism relies on grooves - turning is very rough - I have several); a smoother turning version is known as the Spindle Domino (I finally acquired one); there is also a Russian Domino which has a more complex internal mechanism and turns more smoothly (I found one!); there are also recent black and white versions, and a reproduction of the old design with pips, based on the new 2x3x3, made by Smaz. QJ has produced a 2x3x3 cylinder.

Also shown are the smaller vintage clone dominos, and a version in the shape of a Chinese Knot.

Solving the Domino

You only need four algorithms, in four steps:

1) Solve the edges in one 3x3 layer (white) intuitively

2) Hold this layer D, and drop its corners into place -
Up Right Front -> Down Right Front using the "Corner Drop" CD:

R U R U' R

If the colors don't line up, you need to swap the L and R edges.
If a D corner is in the wrong place, drop something else on it.

3) Permute the U corners (they won't need orientation)

If "headlights" exist, turn U so they face left. Do
R U R U' R * y' * R U' R U R

The last 5 moves are CD backwards, DC
so you can try to memorize this algorithm as CD y' DC

Repeat step 3 if necessary.

4) Permute the U edges (they won't need orientation)

  • Swap opp. UF and UB: (R U2)x3

  • Swap adj. UF and UR:
    R U R U R * U2 R U2 * CD

    The first 5 moves are CD with no primes CDnp

    so this alg can be memorized as CDnp U2 R U2 CD

  • H-perm:
    MUM U2 MUM

  • Z-perm B<->R & F<->L:
    MU (MF)x2 U'M
2x3x4 - Garrett Ong


 2x3x4
Designed by Garrett Ong [T] [S]
Garrett's 2x3x4 won the Summer Puzzle Building Contest. It's a great achievement at its price point (under $60).
2x3x4 - Mf8 (mass prod.)

 2x3x4
mass-produced commercial version from DaYan / Mf8
I modified mine with the 3 extra split edges that eliminate hidden bandaging and restore full functionality
2x3x5 - MattStudiosPuzzles

 2x3x5
- a custom fully functional cuboid twisty, by MattStudiosPuzzles on Etsy.
2x4x4 - Ola Jansson

 2x4x4
by Ola Jansson (Olz). I have a version 3.25, made by Ola. Here is a video of version 3.1 which looks similar: [Y]; The original was much larger: [Y]; [T] [S] Solve video: [Y]

This is a very nicely finished, stable and incredibly smooth-turning puzzle, and it shape-shifts.

2x4x6

 2x4x6
A black and a blue copy of the 2x4x6 cuboid twisty puzzle -
designed by Hunter Palshook, produced by Calvin's Puzzle
2x5x5


The comparison photos show the 2x5x5 with the KHD/Olz 1x4x4, and the original hand-made 1x3x3 from Okamoto.

2x5x5
Designed by Ola Jansson, made by Karl-Heinz Diekmann
2x6x6


 2x6x6
Hand-made Custom 2x6x6 Cuboid Twisty Puzzle - Traiphum Prungtaengkit [FB]
Cuboids - 3-Layer
3x3x3

 3x3x3
[See main Hexahedral section]
3x3x4

 3x3x4
4.13 x 1016

issued by James Lee at Cube4you
Previously only available as an expensive hand-made custom creation. This is based on Jin Kim's design - get STLs by Tom van der Zanden at TwistyPuzzles.com Forums, thread #12134.

Proportional FF 3x3x5

 3x3x5 (Proportional)
made by Smaz
Cubic 3x3x5

 3x3x5 (Cubic)
From Cube4You.
Note: this design was first sold by Adam Cowan and Jason Smith.
3x3x6 (Non-proportional)

 3x3x6 - Witeden
Proportional FF 3x3x7

 3x3x7 (Proportional)
Witeden 3x3x7
Cubic 3x3x7

 3x3x7 (Cubic)
From Cube4You.
Cubic 3x3x9

 

3x3x9 (Cubic)
Also 3x3x9 Roadblock I - black
3x4x4

 3x4x4
Ayi's 3x4x4
3x4x5 - Tom van der Zanden (custom)
3x4x5 - Mf8 (mass prod.)

 

3x4x5
Designed by Tom van der Zanden.

I have a Shapeways print in black, put together by Tom. I also have a transparent instance of the mass-produced version by Mf8. Both turn very nicely, and both shape-shift.

3x5x5 - Floyd Newberry (custom)

 3x5x5
A custom FDM 3D-printed 3x5x5 cuboid twisty puzzle
made by Floyd Newberry [T]
Not loose and turns great.
I love the purple material and the custom hollow stickers!
3x5x7 - Traiphumi Prungtaengkit (custom)

 3x5x7
made by Traiphumi Prungtaengkit
Solid, smooth, and beautiful - as usual!
See a nice article on cuboids by Kevin Sadler at Kevin's Puzzlemad blog.
Kevin calls the 3x5x7 the ULTIMATE cuboid.
Cuboids - 4-Layer
4x4x4

 4x4x4
[See main Hexahedral section]
4x4x5

 4x4x5
Ayi's Toy [T] [W]
4x4x6

 

4x4x6
Tom van der Zanden designed a 4x4x6 cuboid [T],
which has now been mass-produced by Calvin Fan and marketed under his Calvin's Puzzle line [T].
4x5x5

 4x5x5
Ayi's 4.5.5
ayistoy.com

 

Octahedral Twisties

F V E
O1O2O3+ O1O2O3O4+ O1O2



N/A
Babyface
Edge
Matching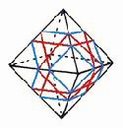





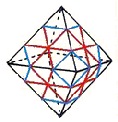
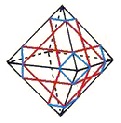
N/A
Trunc.
Dino
Octa


N/A
C-O
Dino
Octa




N/A
trivial
tips
only

Octa
form of
Pyra-
middle









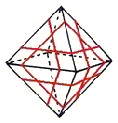
Pyra-
middle
w/ deep
cuts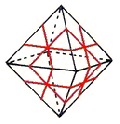










 

Face-turning Order 1
The FT-O1 Octahedron has a single cut midway between each pair of parallel faces.
Skewb Diamond - GB 4.1.1
138,240 - Uwe Meffert - Skewb core

Skewb Diamond, also a clone from Mozhi, in white.
In this Skewb mod, the orientations of the Skewb corners do not matter (they have become the monochrome triangular face centers) but the orientation of the Skewb faces do since they have become the four-color tips.
Jaap's page

Skewb Diamond - various truncations

 Various truncations of the Skewb Diamond - Rugby ball and Treasure Box.
Skewb Hex - Tony Fisher - Meffert

 Meffert's Skewb Hex
Designed by Tony Fisher - used to be a hand-made custom mod. A Skewb Diamond with the tips truncated (but not all the way). Truncating the tips all the way gives a cuboctahedron shape - this has been made as a custom mod by Carter Tarrer and is called the "Mama Skewb." (Shown but I don't have it.) Note how in either case the orientation of the square faces must be evident in order for the puzzle to be non-trivial - in Tony's case the sides of the frustums are colored; in Carter's case each bare square face is colored along its edges.
Square Octahedron - Mozhi

 "Square Octahedron"
This version of the Skewb Diamond (actually the Mozhi brand diamond) has build-ups on the triangular faces which make their orientation matter, so it has more states than the Skewb Diamond.

Face-turning Order 2
Order 2 Octahedra have 2 cuts between each pair of parallel features.
Similarly to other Order 2 puzzles, these cuts can be spaced in three distinct arrangements.

Face-Turning Octahedron (FTO)- GB 4.1.2
3.14*1022

Face-Turning Octahedron (FTO)

(on the left, compared to the Magic Octahedron on the right)

Also known as the "8-axis octahedron."

When this puzzle first appeared, I went through some machinations to obtain one from an Asian contact - it is shown in my comparison photos here. Now they are produced by Lanlan and are available for around $12.

Solving the FTO

You really only need one algorithm, but you'll have to be thoughtful about how to apply it in sequences towards the end of the solve. I find this makes solving the FTO fun.

Hold the puzzle so one triangular face is on top, pointing away from you - as in the first Lanlan photo where green is on top and white faces you.
The top is U. The face on the front right is R (purple in the photo) and the face on the front left is L (blue in the photo).

The algorithm is: (R U R' U)x2

It moves the 3 face centers and the 3 edges in the top layer clockwise one position, without disturbing the rest of the puzzle.
If you instead want to move them counterclockwise, substitute U' for every U - the rotation goes in the direction you rotate U.

The solution process is:

1) Solve the corners, intuitively. Corners only have two orientations, not four. A handy alg to twist both the UR and UL corners 180 in place is: R U' R' U  R' L R L'

2) Move all face centers into position, using the alg with "slice" setup moves. At first you can simply use a slice move to directly place a center where needed, but eventually you'll have to use a slice move to move the target location into an orbit where a needed piece sits, place the piece using the alg, then move the slice back, carrying the newly placed piece into its proper position. You may even have to use the alg as a first step, to rotate correctly placed centers out of the way, or a needed center into position in preparation for putting it into the target slice. But these sequences shouldn't be too difficult to figure out!

3) Move all edges into position, using the alg - but avoid setup moves other than sequences of interlocking alg moves, lest you mess up the placed centers. You do this after step (2) since although the alg will move the centers, by now they are indistinguishable and interchangeable. This is the hardest step, since you have to figure out the ballet of swaps and temporary displacements to get the last few edges into place together.

Truncated Face-Turning Octahedron (FTO)- LanLan Hydrangea

 LanLan Hydrangea - Truncated Face-Turning Octahedron
Dino Octa - GB 4.1.3 - (Okamoto) Mf8


 Mf8 Crazy Octahedron Standard - no circle faces
This substantial puzzle is a nice implementation of the "Dino-Octa" face-turning octahedron design (GB 4.1.3) originally hand-made by Katsuhiko Okamoto in 2006. [T]
Out of the box it is prone to catching, though.
I prefer stickerless twisty puzzles like this when available.
Face centers remain in place.

Also shown is the Mf8 Crazy Octahedron Venus - all circle faces
The four other "planets" (Mercury, Mars, Jupiter, and Saturn) can be made by combining pieces of the Standard and Venus puzzles. [Y]

Rainbow Octahedron


 A pair of deceptively look-alike custom-3D-printed twisty puzzles:
an Edges-Only Trajber's Octahedron, and a Rainbow Octahedron -
designed and made by Kevin and Jenna Uhrik.
I had wanted examples of these two puzzles for a while,
and asked Kevin to design "twins" for me - he produced this beautiful and satisfying pair.
They have inlaid tiles, and turn very well.
Kevin posted a video of the puzzles. They have worn in nicely and turning is much less "scratchy" than it sounds in the video.

The Rainbow Octahedron (on the right) is so-named because in the past it was made by building up a Rainbow Cube,
which used to be common but is now fairly rare in its own right.
The Rainbow Octahedron seems to have been invented by Jürgen Brandt circa 2003.
In 2008 Geert Hellings had the idea for extensions that could be glued on to Rainbow Cube faces - I remember saving the STLs in the hopes of someday printing them myself so I could make a Rainbow Octahedron - but in the end getting this nice puzzle from Kevin proved easier.
The Rainbow Octahedron is face-turning and is very easy to solve without algorithms.
An inexpensive version has been mass produced and is called the Fangshi Limcube 2x2 Transform Pyraminx BaMianTi II - Octahedron II.

Fangshi Limcube 2x2 Transform Pyraminx BaMianTi II - Octahedron II

 Fangshi Limcube 2x2 Transform Pyraminx BaMianTi II - Octahedron II
This is a small and curvy-cut but very nice mass-produced implementation of the Rainbow Octahedron. It can be found for about $10. The Rainbow Octahedron is fairly easy to solve - only the edges permute - it can be done with no algorithms. I really like this one!
Master Skewb Diamond - GB 4.1.4

 4.1.4 "Morphix" Octa - face centers move
an FTO with exposed centers
aka Master Skewb Diamond, made by "kwsjack054" aka Wen Hsi Kang in May 2011 [TP Museum] [T] [Mf8 BBS]

Also Clay & Eva in June 2010 [T]

Face-turning Order 3+
Master FTO - GB 4.1.5

 O3=4.1.5 Master FTO
Made by Timur [T] [T] [T] [T] [S]

Also by Tom van der Zanden [S]

I bought a 3D printed instance made by Tom.

Mf8 Master FTO

 Mf8 Master FTO
A very nice mass-produced master FTO.
O3 Elite FT Octahedron

 Elite Octahedron - "El Cubitero" 2020 [TP Museum] [T] [V]
Order 3, 4 layers
O4 Royal FT Octahedron - Mouflin

 Royal Octahedron - Rafael Mouflin 2017 [TP Museum]
Order 4, 5 layers
Vertex-turning Order 1
Okki / Gem

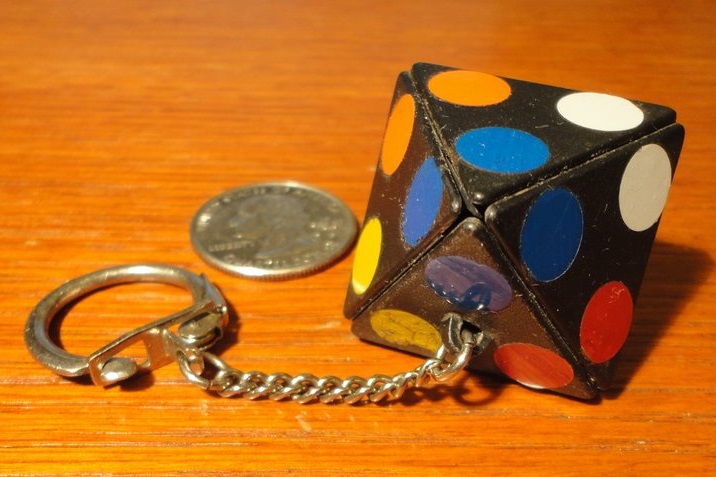
 Okki - a vintage keychain twisty puzzle - I found an original!
Essentially a 2x2x2 where all eight corners have been beveled away. Like the 2x2x2 corners, its faces don't show orientation without coloring. Grabbing a corner and twisting its four surrounding triangles is the same as grabbing a 2x2x2 face and twisting its four surrounding corners.
Pyradiamond (Meffert)

 PyraDiamond, Meffert's version of the Okki/Gem.
4D8

 The 4D8 Cube was invented in 2001 by Heinz Molidor, an Austrian engineer. It was presented in 2009 at the Nuremberg Toy Fair and in 2010 on Bavarian Radio. The 4D8 twists like the Pyradiamond (2x2x2), but in addition each face has a frustum that can be rotated in place. The object is to get the same color on all facelets pointing in a particular direction (the photo shows it solved). [T]
Vertex-turning Order 2
Magic Octahedron - GB 4.2.2
8.23*1018 (including the trivial tips)

Magic Octahedron
Also a more recent larger version by DaYan
Also comparison shot showing (L to R, front to back): original Cristoph's Magic Jewel, recent Gem, original Magic Octahedron, recent DaYan, face-turning octahedron.

Also known as the "6-axis octahedron" or the "corner turning octahedron" (CTO).

Christoph's Magic Jewel
2.0*1015 - Christoph Bandelow - 6-armed spider

Christoph's Magic Jewel - a Magic Octahedron minus the tips
I finally found one at IPP 29 in SF.
Also, the DaYan Gem from China.

Trajber's Octahedron - GB 4.2.1
1.35*1019

Trajber's Octahedron
The Trajber's Octahedron is a vertex-turning puzzle and has a 3x3x3 cube core.

I have a hand-made version purchased from David Calzone - cast pieces molded from 3D-printed masters. Also shown is a mass-produced Trajber's, from QJ.

The group shot shows various kinds of octahedral twisty puzzles - the vertex-turning Magic Octahedron, the Trajber's, Meffert's Skewb Diamond (face-turning), and a face-turning octahedron from Taiwan (the next higher order from the Skewb Diamond).

The Trajber's solves like a 3x3x3, except 3x3x3 corners which are the triangular face centers on the Trajber's don't need orientation but 3x3x3 face centers which are the corners on the Trajber's do, so you need the supercube face centers algorithms.

These are the Supercube face algorithms - algorithms exist to rotate a single face center by 180, or a pair - one by 90 and another -90.

U180: ( (U R L U2) R' L') x2

U90 & F-90: F B' L R' - U D' F' U' D - L' R F' B U

U90 & D-90: R L' F2 B2 R L' U R L' F2 B2 R L' D'

Truncated Trajber's Octahedron - Tanner Frisby
6.59*1015

Truncated 3x3x3 Trajber's Octahedron
Made by Tanner Frisby.

On the truncated Trajber's the 3x3x3 face centers which are the Trajber's corners don't need orientation so you won't need the supercube algorithms. As on the normal Trajber's the 3x3x3 corners which are the Trajber's triangular faces do not need orientation, so the truncated Trajber's is simpler than a 3x3x3.

Void Trajber's / Holey Octahedron - TomZ

 Void Trajber's / Holey Octahedron - made by Tom van der Zanden
In 2009 Tom also created a "holey" Trajber's.
In 2012 David Pitcher created the Octadot, which is also equivalent to a Trajber's.
Evgeniy Grigoriev offers both a mini Holey Trajber's / Void Octahedron, and Pitcher's Octadot.
Edges-only Trajber's - John Lin, Kevin Uhrik


 Edges-only Trajber's - John Lin, Kevin Uhrik

A pair of deceptively look-alike custom-3D-printed twisty puzzles:
an Edges-Only Trajber's Octahedron (left), and a Rainbow Octahedron -
designed and made by Kevin and Jenna Uhrik.

The EO Trajber's is vertex-turning and solves like a 3x3x3 but can end up in parity states.
Super-center algorithms may be needed to resolve the parity and are needed for corners on the full Trajber's Octa.
An EO Trajber's was made by John Lin in 2008 and this was my inspiration.

Edges-only Trajber's - Evgeniy Grigoriev

 In 2009 Tom van der Zanden made a true Edges-Only Trajber's Octahedron variant he calls the Dino Octahedron,
hiding the centers.
I have a similar true Edges-Only example, the Jewel Octahedron by Evgeniy Grigoriev (Grigorusha), which I picked up in June 2018.
Evgeniy modeled his JO after an Alexander's Star, but it is isomorphic to Tom's version.
Pyraminx Diamond (Corners-only Trajber's)

 Pyraminx Diamond - 8 color version
designed by Oskar van Deventer, based on the "Rob's Pyraminx"
issued by Meffert

Also shown is a Trajber's Octahedron family shot including a hand-made (cast, not 3D-printed) Trajber's Octahedron (right foreground) made for me several years ago by David Calzone of the Twisty Forums, and the Pyraminx Diamond (left background) (aka Rob's Octahedron) designed by Oskar van Deventer and issued by Meffert - which is a Corners-Only Trajber's Octahedron.
Note that, while the Edges-Only form can have faces as with Kevin's (Lin's) version, or can omit the faces as in Evgeniy's Jewel Octahedron or Tom's Dino Octahedron, the Corners-Only form - the Pyraminx Diamond / Rob's Octahedron - needs the faces, which permute during vertex turns, otherwise the puzzle becomes a trivial set of six turning but non-permuting vertices.

Vertex-turning "Morphix" Octahedron

 The VT "Morphix Octa" has trivial tips - face centers remain in place. Not made AFAIK.
VT O2 Coin Octahedron

 Coin Octahedron - made by Linxiao Xu in 2020, also by Kevin Uhrik [T] [W]
The Coin Octahedron comes closest to the Morphix Octa shown above - here, the tips turn only with the underlying segments - so there are no trivial tips. Also, there are no little edge pieces. The face centers remain in place, and the face segments can be permuted. As an added function, here the inner faces with their three surrounding segments can be rotated.
Vertex-turning Order 3+
Lolo's Octahedron - GB 4.2.3 - Kevin Uhrik

 Lolo's Octahedron, custom-made by Kevin Uhrik.
Hexic (Lolo's Octahedron - GB 4.2.3) - Kevin Uhrik

 Hexic - by Kevin Uhrik at The Puzzle Artists on Etsy
A Dogic-themed Lolo's Octahedron.
Purchased in 2019.
Substantial and very nicely made, in beautiful colors.
I have an older Lolo's Octahedron hand-made by Kevin - Kevin and puzzle-making technology have come a long way since then!
Fangshi Limcube 2x2 Transform Pyraminx BaMianTi I - Octahedron I

 Fangshi Limcube 2x2 Transform Pyraminx BaMianTi I - Octahedron I - a mass-produced Lolo's Octahedron. Shown in comparison with my custom Lolo's Octahedron made by Kevin Uhrik.
Okki + Magic - GB 4.2.4 - Order 3 - Andreas Nortmann

 Okki + Magic - GB 4.2.4 - Andreas Nortmann [T]
This is a Master Trajber's without the centers.
It can appear to be a Magic Octahedron without the trivial tips, but unlike that puzzle, this one also has the Okki cuts.
Master Trajber's Octahedron - GB 4.2.5 - Order 3

 4x4x4 Master Trajber's Octahedron, also version with colored pieces. [T] [Y]
Master Octahedron - GB 4.2.6 - Order 4


 The Order-4 Master Octahedron - GB 4.2.6
Made by Aleh (2005) [T], Scott Bedard (2008) [T] [T], Garrett Ong [T] [S]

I received my copy in a trade with Kevin Uhrik. This is a hand-cast version made from Scott Bedard's design and tweaked by Kevin.

In 2020, Kevin sent me a revised Master Octahedron, shown below the original. It looks beautiful and functions great!

Also shown is a comparison of Kevin's Order-4 vertex-turning Master (Magic) Octahedron (left), with Timur Evbatyrov's Order-3 face-turning Master FTO (Face-Turning Octahedron) of 2010/2011, and a family shot of the original Magic Octahedron (left foreground) and FTO (right foreground) with their higher-order siblings.

Professor Trajber's - Ryan Thompson

 The Order-4 Professor Trajber's - Ryan Thompson - made from a 5x5x5 [Y]
Professor Trajber's ("Curvy 5x5 Octahedron") - TwistyTurtle

 Professor Trajber's (Curvy 5x5 Octahedron) - by "TwistyTurtle"
Purchased from and custom made by Chewie's Custom Stickers
6x6x6 Trajber's - Minh Thang Vo

 6x6x6 Trajber's - Minh Thang Vo
Aleh's Master Octahedron

 O4 Trajber's-like Master Octa made by Aleh [T]
Edge-turning Order 1
The 24 Octahedron - GB 4.3.3

 Made as a custom build, based on a shells core designed by Matt Shepit.

Magnetic core versions have also been produced. [T] [T]

A version based on extensions to a Chromium Cube was made [T]

My example was made for me by James Li, based on his Chromium mechanism. Shown with some of my other custom octahedral puzzles.

Edge-turning Order 2

GB 4.3.6 - Shallow-cut ETO (No name.)

 A shallow-cut Edge-Turning Octahedron - cuts meet in face centers. Truncate the tips and you get the DaYan Gem.

In 2010 "kwsjack" of Taiwan modded a Gem back to an octahedron, with overlapping tips. He referred to it as his "Edge Turning Octahedron" [MF8 BBS] [MF8 BBS]

DaYan GEM I

 The DaYan Gem (an edge-turning truncated octahedron, related to GB 4.3.6)
Eitan's Edge-turning Octahedron (ETO) - GB 4.3.1 - Eitan Cher

 Here is Eitan's Edge-Turning Octahedron (ETO) - announced on the TP forums. Equivalent to Gelatinbrain 4.3.1. Available from Eitan's Shapeways shop. First shown by David Calzone back in 2009. Congrats to Eitan for making this available! The design moves well, is stable, and is a nice size. The puzzle came very nicely stickered.

Shown in comparison with other octahedral twisty puzzles:

From top to bottom, left to right: Meffert's Skewb Diamond (order-1 face-turning octa); DaYan Gem I (edge-turning trunc. octa); order-2 vertex-turning octa; order-2 vertex-turning trunc. octa; order-3 vertex-turning master Trajber's; Meffert's Hex Skewb (order-1 face-turning trunc. octa); order-2 face-turning octa; Eitan's ETO (order-2 edge-turning octa); vintage Magic Octahedron (order-2 vertex-turning octa); QJ Trajber's (order-2 vertex-turning); hand-cast custom Trajber's made by David Calzone; QJ 3x3x3 octa (sort of hybrid edge- and vertex-turning); Octaminx custom made by me; Meffert's Pyradiamond (order-1 vertex-turning octa); vintage Christoph's Magic Jewel (order-2 vertex-turning trunc. octa); Lolo's Octahedron custom-made by Kevin Uhrik (order-3 vertex-turning octa); Truncated Trajber's custom-made by Tanner Frisby.

I still would like to find: a Rainbow octa, a 24 octahedron, a Dino octa, a Master octa, a Master FTO, and a Professor Trajber's. Maybe a Square-1 and/or Square-2 octa, too.

Curvy Copter Octahedron - Order 2 - Seth Holiday

 Curvy Copter Octahedron by Seth Holiday [T]
Also see the hybrid O2,O1 Leaf Octahedron by Kevin Uhrik, below - that puzzle resembles this, but adds the Okki cuts.
GB 4.3.2 - "Octahedral Toru"


 Octahedral Toru - by Vladi Delimollov
This is an example of the edge-turning order-2 octahedron GB 4.3.2. Placing the cuts slightly deeper than Eitan's ETO (GB 4.3.1) results in hexagons on the faces.
3D printed by and purchased from Chewie's Custom Puzzles.
YouTube video - shows jumbling.
It catches a little but it is nice and solid. I really like it!
Edge-turning Order 3+
GB 4.3.5 (No name.)

 O3 4.3.5 - not made AFAIK.

Hybrid O1,O1
Omitting the 24 Octahedron, combine the FT O1 Skewb Diamond with the VT O1 Okki.

FT O1 Skewb Diamond + VT O1 Okki (No name)

Looks like a Lolo's Octahedron, but the faces turn and the tips do not rotate.

FT O1 Skewb Diamond + VT O1 Okki
Not made AFAIK.

Hybrid O2,O1
Lots of empty slots here - many of these combinations probably wouldn't be compatible.
Adding the Okki cuts to the FT O2 puzzles probably won't work well if at all, though they might work with the VT and ET puzzles.
Adding the VT O1 Skewb Diamond cuts to most of the O2 puzzles also doesn't seem feasible.

  FTO FT Dino FT Rainbow FT Mast Skewb VT Magic VT Trajber's VT EO Trajber's VT CO Trajber's VT Morphix (Coin) Octa Shallow ETO Curvy Heli
 
FT O1
Skewb
Diamond

Skewb Diamond + FTO = Master FTO 		                   
VT Okki
       
GB 4.2.4 Nortmann
VT Okki + VT Trajber's = Master Trajber's 		       
Leaf Octahedron

O2,O1 Leaf Octahedron - Uhrik

 Leaf Octahedron - designed and 3D printed by Kevin and Jenna Uhrik
See their Etsy shop The Puzzle Artists.
At its heart this is a 2x2x2 Pyradiamond, but it is hybridized with an Order-2 edge-turning octahedron having curvy cuts and no corners.
O2,O2 FTO + Magic Octa = Comboctahedron - Eitan Cher

 FTO + Magic Octa = Comboctahedron - Eitan Cher [T] [T]
O3,O2 Master FTO + Magic Octa = Hybrid Octahedron - Kevin Uhrik

 O3,O2 Master FTO + Magic Octa = Hybrid Octahedron - Kevin Uhrik [T] [W]
Only two cuts per vertex axis; three cuts per face axis.
Geared
Gear Octahedron - LanLan

 Gear Octahedron - from LanLan based on Oskar van Deventer's design
Gear Octahedron - Timur / Calvin

 Gear Octahedron - from Calvin's Puzzle based on Timur Evbatyrov's design
Shapemods
3x3x3 Octahedron - QJ

 3x3x3 Octahedron mass-produced by QJ
Octic

 Octic versions I, II, III, IV
purchased from Zoneden.
Four versions of a nicely done shape variation of a cross cube.
Octahedral Mixup series - Witeden

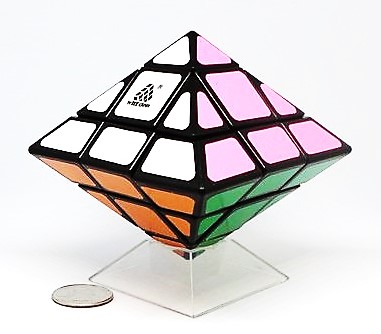
 Series of Octahedral Mixup puzzles, by Witeden
I have the Octahedral Mixup I, which is similar in appearance to (though larger than) the QJ 3x3x3 Octahedron.
The others are shown for reference and include: Octahedral Mixup I Plus, Octahedral Mixup II (which looks like a Trajber's), III, IV, and the Mike Armbruster version.
Octaminx - Tony Fisher - Rob Stegmann

 I completed my first real twisty mod! I made an Octaminx (a design originated by Tony Fisher) from a couple of old Tomy Pyraminx puzzles. This is an "old school" mod - done with a saw, and various other implements of destruction - not casting. I've got the sliced and abraded fingers to prove it. I hand-cut the stickers myself.

As of Feb. 2011 my first Octaminx (this white one) is in the collection of Laurie Brokenshire. I still have another (imperfect but functional) black one I made.

Edgematching
Tantrix The Rock
1*1018 - "over a billion billion"

Tantrix The Rock
A truncated octahedron.
This type of 3D edgematching puzzle is included here because I consider them "faces-only" versions of twisty polyhedra - no corners and no edges.
Tantrix Home Page
Jaap's page

Hungarian Rock

Hungarian Rock Hungarian Rock

Hungarian Rock - a vintage 3D edgematching twisty puzzle
Related
Dino Star

 Dino Star (blue) - a vintage commercially produced puzzle.

A stellated octahedron with a tip on each face. An inverted edge piece rides at each border between adjacent tips, and moves as the tips are twisted in place. Solve by ensuring that all 3 edge-halfs showing around each tip are the same color.

Verypuzzle Clover Octahedron

Clover Octahedron Clover Octahedron Clover Octahedron

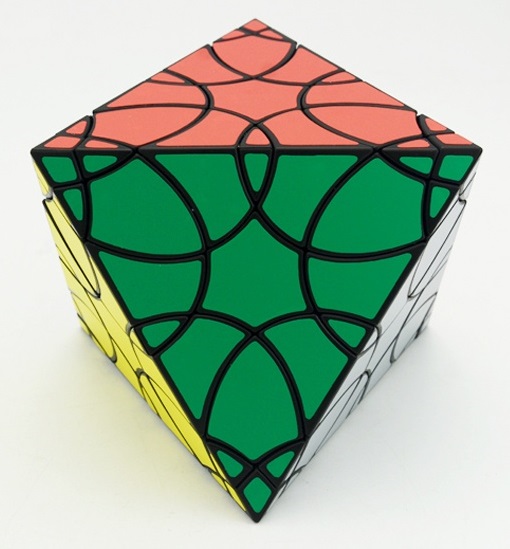
Clover Octahedron - by Verypuzzle
Verypuzzle Clover Octahedron Fragmentation

Clover Octahedron Fragmentation Clover Octahedron Fragmentation

Clover Octahedron Fragmentation - by Verypuzzle
Clover Octahedron - Lanlan

Clover Octahedron - Lanlan Clover Octahedron - Lanlan Clover Octahedron - Lanlan Clover Octahedron - Lanlan

Clover Octahedron - Lanlan
Triqueta Octahedron

 Triqueta Octahedron - a custom 3D-printed twisty puzzle from Lycharmodpuzzles on Etsy.
Four solid faces turn, scrambling segments on the remaining four faces,
including those teeny tiny face centers.
I've scrambled mine in this pic.

Dodecahedral Twisties

See Dodecahedral Puzzles in the TwistyPuzzles Museum

F V E
O1O2
Start 2 cuts at opposite faces and move them inwards...		O3O4+ O1O2 O1O2











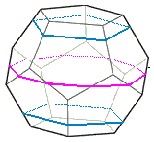
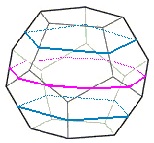
Not
 
Made






N/A
Pentult
w/ Mega






Exa-
Minx
5+5 cuts

Zetta-
Minx
6+6 cuts














 

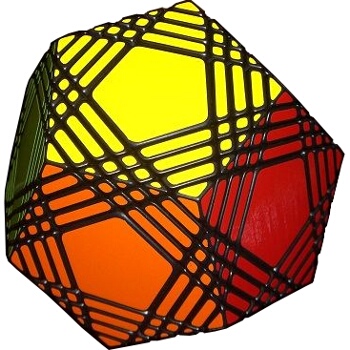
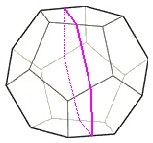
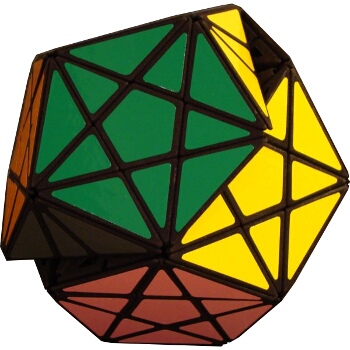
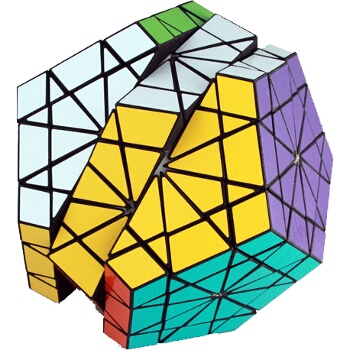
Face-turning Order 1
Pentultimate - GB 1.1.7

 For the last puzzle in 2010, I received Tom van der Zanden's excellent Pentultimate.

You can buy one, and several other great twisty puzzles, at Tom's Shapeways shop.

This is the order-1 face-turning dodecahedron. It has six cuts, all of which pass through the center of the puzzle, midway between pairs of opposing faces, and are great circles on the circumscribed sphere. Each divides the puzzle into two halves.

It is an engineering design masterpiece and employs a sophisticated "shells" mechanism. The shells build upon a Megaminx, through a Pyraminx Crystal, Master Pentultimate, to the outer Pentultimate. In a shells mechanism, the pieces of an inner shell hold in the pieces of the next shell out. For example, the Pyraminx Crystal has two shells - an inner Megaminx and the outer Crystal. The faces of the inner Megaminx hold in inner edges, which in turn hold in the outer Crystal corners, which hold in the outer Crystal edges.

The Pentultimate is 25mm (1") on an edge, and is the same size as a QJ 3x3x3 dodecahedron. The design explores the limits of economical miniaturization within the 3D printing process, yet the puzzle is not fragile and is quite comfortable to hold and manipulate. It was announced on the TP Forums here. You can see an image of the complicated internal mechanism in that thread.

For information on the earlier impressive albeit fragile so-called "knucklehead" mechanism pioneered by Jason Smith, who designed and constructed the first working version of this puzzle, see an article at Jason's Puzzle Forge website.

Brandon Enright gives a fairly simplified solution process in a video.

Void Pentultimate - Mf8

 Void Pentultimate - Mf8
Face-turning Order 2
Flowerminx / Kilominx - GB 1.1.12
2.36*1025 - Megaminx core

Flower Minx - from Mefferts, designed by David Litwin. This is a corners-only Megaminx, aka "Kilominx."
Equiv. to Impossiball.

Shengshou Megaminx 2x2 (Kilominx) - GB 1.1.12

 Shengshou Megaminx 2x2 (Kilominx)
Megaminx - GB 1.1.1

Modern Speed-Cube Designs
1.0*1068 (12 color version); 6.144*1063 (6 color version)
Kersten Meier, Ben Halpern - 12-armed spider

Megaminx
Tomy version, Meffert's tiled version, tiled Chinese version, stickered black Hong Kong version, stickered white Hong Kong version

Modern speed-cube style Megaminx designs include: DaYan stickerless with corner ridges, Lim Cube Fangshi, QiYi Galaxy Sculptured stickerless, YJ Moyu YuHu R

My favorite is the YJ Moyu YuHu R - be sure to get the R version!

Solving the Megaminx

Here is how we'll refer to face turns.
The second diagram is looking at the U face from the top.
All algorithms except the single edge placement
algorithm assume this view.

The solve takes place in stages:

  1. Place top edge pieces to create a star on U
    (usually the white face).
  2. Place 4 out of 5 2nd layer edge pieces
  3. Use last L2 edge as keyhole, place top corners
  4. Place last L2 edge - use 3x3x3 Edge algorithm
  5. Place L2 corners
  6. Place L3 edges using Edge algorithm
  7. Place L3 corners
  8. Place L4 edges using Edge algorithm
  9. Last Layer (LL) - HOLD IT ON TOP and:
    1. Flip (Orient) Edges
      (get all gray on top)
    2. Cycle (Permute) Edges
      (move to correct positions)
    3. Cycle (Permute) Corners
    4. Flip (Orient) Corners

 


Edge algorithm - similar to 3x3x3
D' R' D R * D F D' F'


Flip (Orient) Edges
CCW: F R U R' U' F'

CW: F U R U' R' F'


Cycle (Permute) Edges
CCW: R U R' U * R U' U' R'

CW: R U U R' * U' R U' R'

 


Cycle (Permute) Corners
CCW: U R U2' L' U
U R' U2' L U

CW: U' L' U2 R U'
U' L U2 R' U'


Flip (Orient) Corners:
A. Turn U to move unsolved corner
to asterisk position at FR
B. Perform R' D' R D
until solved. ALWAYS DO ALL FOUR MOVES.
Repeat steps A and B until all corners are solved.
Hungarian Supernova

 Original Hungarian Supernova in clear cylindrical package.
Also have a Hungarian Supernova re-issue with its white box.
Note how the tips of the stars on the faces of the Supernova make points rather than the "snub" edges of the Megaminx. The tiled Chinese Megaminx also has pointed stars, but that puzzle turns horribly and its plastic is brittle, while the Supernova turns well and is of good quality.
Holey Megaminx / Void Megaminx - Lee Tutt / Meffert

 The Holey Megaminx from Mefferts (in black and white), designed by Lee Tutt.
Pyraminx Crystal - GB 1.1.3
1.68*1066 - A build-up of the Megaminx, without centers.

Meffert's Pyraminx Crystal (black tiled version, and black and white stickered versions)
First patented in 1987 by Uwe Meffert: DE8707783 (U1).
Katsuhiko Okamoto had created a version he called the Mega Crystal.
Aleh Hladzilin created a version he eventually named the Brilic - he made around a dozen, some of which sold for over $1000. At first he used a Dogic core, then later a Megaminx core.
Noah Hevey has written a nice history of this puzzle - see topic 85537 in the TwistyPuzzles forums. Also see thread 7711 for a discussion of solution methods.
While a twist on the Megaminx moves 5 corners and 5 edges, a twist on the Crystal moves 5 corners and 10 edges.

Starminx I - GB 1.1.5 - Tom van der Zanden

 In 2011, I had the pleasure of meeting Tom van der Zanden [S] at IPP 31 in Berlin.
Tom made me a slightly larger version of his Starminx I [T]. The Starminx is shown in comparison to Tom's Mini-Pentultimate. Previous versions of the Starminx have been made by Drew Cormier [T] and Aleh [T].
Starminx I - GB 1.1.5 - Mf8

 Mf8 Starminx II - in translucent purple
This is a mass-produced version of what the twisty forum knows as the Starminx I, previously custom-made by Aleh [T] , Drew Cormier [T] , and Tom van der Zanden, in mini [T], and larger size [T] . (Mf8 called their Dino-Dodecahedron a Starminx I, hence the naming confusion.)
I finally stickered my purple Mf8 Starminx.
As people have noted, it does not turn as smoothly as Tom's (admittedly much more costly) 3D printed version.
Curvy Starminx - Mf8

 Mf8 Curvy Starminx
Master Pentultimate - GB 1.1.6 - Eric Vergo


 I received a Master Pentultimate designed and made by Eric Vergo. It turns very smoothly. This is a great design! Shown along with Tom van der Zanden's Pentultimate.
(Void) Master Pentultimate - GB 1.1.6 - mass produced by Mf8

 Mf8 (Void) Master Pentultimate
(Shown with optional center panels in place.)
Multidodecahedron - Tom van der Zanden

 A Multidodecahedron by Tom van der Zanden [T] The theory behind this puzzle was discussed by Carl Hoff here.
This is a custom 3D printed puzzle, but the pieces of my copy have been through a "tumbling" process that makes them smooth. [T]
The Multidodecahedron is an outer Master Pentultimate, where the face centers expose an inner Megaminx shell having its own stickers. A full solution entails solving both layers. [T]
Face-turning Order 3+
Gigaminx - GB 1.1.9
3.65*10263

Gigaminx

Originally realized by Tyler Fox. Subsequently made by others. Commercially released by James Lee at Cube4you

Gigaminx - Shengshou

 Shengshou also offers a Gigaminx. (I don't have one.)
Master Kilominx / Hyperminx - Mf8

 Mf8 Master Kilominx (solid colors)
Also known as the Hyperminx
This is essentially a Gigaminx where the central stars have been hidden. The pieces overlap during turns.
Shengshou Master Kilominx

 Shengshou Master Kilominx
Teraminx - GB 1.1.41
1.16*10525

Teraminx

Originally designed by Drew Cormier. According to Drew, the Teraminx contains 555 pieces! Produced commercially by Cube4you and Mf8. I got a C4U because of a misrepresentation by a vendor. The MF8 version is superior, and I got one from Meffert.

Teraminx - Shengshou

 Shengshou also offers a regular Teraminx with flat sides. (I don't have one.)
Elite Kilominx - Shengshou

 Elite Kilominx - Shengshou
Petaminx
3.16*10996

Petaminx
This had been a very expensive custom-made puzzle (in the $3000 price range), designed by Drew Cormier. However, it has been mass-produced (at the $200 - $250 price range) by Mf8.
(Included for reference to show number of positions - I don't have this.)

Vertex-turning Order 1
Halfminx aka Drew's Chopasaurus - GB 1.2.9 - Drew Cormier

 The order-1 vertex-turning dodecahrdon is the "Halfminx" - made by Drew Cormier, who called it the "Chopasaurus." [T]
I don't have this. The closest commercially available puzzle is the Skewb Ultimate - see below.
Skewb Ultimate
1.0*108 - Uwe Meffert

Skewb Ultimate
Jaap's page

The Skewb Ultimate is the "most difficult" of the Skewb family - every piece has a proper orientation, unlike, for example, the face centers on the Skewb.

The hierarchy is:
PositionsMoves to
Antipode		Puzzle
100,776,96014Skewb Ultimate
3,732,48012Halpern-Meier Tetrahedron
3,149,28011Skewb
933,12011Pyraminx
138,24010Skewb Diamond
2,1606Meffert's (4 color) Beachball

Vertex-turning Order 2
Dino Dodecahedron - GB 1.2.1 - Mf8 (their Starminx I)

 A Dino Dodecahedron (aka Dinominx) by Mf8 (they call it a Starminx I), purchased from hknowstore.
This puzzle was first proposed by Lukeharry then made by Kevin Uhrik, now mass-produced by Mf8. [T]
I solve this with no algorithms - it's a fun puzzle. Also quite large - larger than a Pyraminx Crystal.
Rediminx - Moyu

Rediminx by Moyu
This puzzle was designed by Justin Costa and mass-produced by Moyu. It is a dodecahedral form of Oskar's Redi Cube.
I like it because it can be solved intuitively - however near the end, a couple of algorithms may come in handy to reduce flailing...

Flip edges A and B in place - ADJACENT.

L l r   U' R U   R' r' l'   U L' U'

It works like this...
walk A over to the r orbit: L l r
move A's target slot over to the r orbit: U'
put A in place: R
now put B in position to walk the other way: U
walk B over to the l orbit: R' r' l'
move B's target slot over to the l orbit: U
put B in place: L'
fix U: U'
Flip edges A and B in place - NON-ADJACENT.

l D   L' R'   r R   r' D'   R L   l' L'   R' L

It works like this...
walk A over to the r orbit: l D
move A's target slot over to the r orbit: L' R'
put A in place: r
now put B in position to walk the other way: R
walk B over to the l orbit: r' D'
move B's target slot over to the l orbit: R L
put B in place: l' L'
fix L and R: R' L
Curvy Dino Megaminx - designed by AJ Lu, produced by Mf8

Curvy Dino Megaminx - designed by AJ Lu, produced by Mf8
Adding another layer to the Rediminx.

Proper Dino Dodecahedron - Delimollov

Proper Dino Dodecahedron - designed by Vladi Delimollov, made by Chewie's Custom Puzzles.
Vladi's version of the Dino Dodecahedron omits face centers and corners, showing only edge pieces. This puzzle fills one of the slots shown in my dodecahedral puzzles family chart in the lower right - the vertex-turning regime of the edges-only form without centers.
Since there are no fixed face centers visible, remember the color arrangement and beware of nasty parity cases!

Pentagram - GB 1.2.3 - Eric Vergo

 I bought the 1st copy of Eric Vergo's Pentagram puzzle - first announced at the TwistyPuzzles forums. It is an order-2 vertex-turning dodecahedron, designed by Eric and 3D printed by Shapeways. It is the same size as the Meffert's Pyraminx Crystal. You can buy a copy at Eric's Shapeways shop.

There is an online video review of this puzzle on YouTube.

Pentagram - GB 1.2.3 - Eric Vergo

 Pentagram designed by Eric Vergo
produced by Mf8
Once again an expensive 3D printed twisty gets mass produced.
Bauhinia - Mf8

 Bauhinia - produced by Mf8
A "Rex Dodecahedron."
Edge-turning Order 1
Big Chop - GB 1.4.3 - Oskar van Deventer, Jason Smith

 The order-1 edge-turning dodecahrdon is the "Big Chop." As of this writing (June 2013) there is no satisfactory mechanism for this puzzle. Oskar made one using magnets. Jason Smith attempted another interesting mechanism. [T]
I don't have this.
Edge-turning Order 2
Helicopter Dodecahedron - Mf8

 Mf8 Helicopter Dodecahedron, in black
Geared
Gear Minx I

 Gear Minx I - gear twisty mechanism designed by Oskar van Deventer, offered by Meffert.
Gear Minx II

 Gear Minx II - gear twisty mechanism designed by Oskar van Deventer, offered by Meffert.
Circle / Crazy
Crazy Megaminx Plus - Saturn - Mf8

 DaYan/Mf8 Crazy Megaminx Plus Saturn

The fit and turning on the copy I got are very good, and I like the stickerless design and brightly colored plastic. It is about the same size and weight as a Meffert's Pyraminx Crystal. Purchased at the HK Now Store.

Crazy Megaminx - Sengso

 Crazy Megaminx - Sengso
In this puzzle, the small pieces on the faces, surrounding the centers, remain in place during a turn of the face they're in, but they move with a turn of any adjacent face.
Shapemods
2x2x2 Dodecahedron

 A 2x2x2 in the shape of a dodecahedron. Produced by LanLan.
3x3x3 Dodecahedron

 3x3x3 Dodecahedron. Produced by QJ.

More difficult than the regular 3x3x3, since all six centers must be properly oriented.

Edgematching
Dodeca Nona
3.99*1018 - 1122 solutions.

Dodeca Nona
A faces-only dodecahedron.
This type of 3D edgematching puzzle is included here because I consider them "faces-only" versions of twisty polyhedra - no corners and no edges.
12 magnetic pentagonal 2-sided tiles fit to the faces. Each face has the numbers 1 through 5 arranged around its corners - all 24 possible arrangements are included. Place the tiles so that at every vertex of the dodecahedron, the numbers add up to nine.

Mobius

 Mobius
This type of 3D edgematching puzzle is included here because I consider them "faces-only" versions of twisty polyhedra - no corners and no edges.
Related
2x2 Megaminx

 2x2 Megaminx - designed by Gregoire Pfennig and Felixouchon
Produced by WitEden [T]
Very difficult to align and turn.
Verypuzzle Clover Dodecahedron

Clover Dodecahedron Clover Dodecahedron Clover Dodecahedron

Clover Dodecahedron - by Verypuzzle
Alexander's Star
7.2*1034 - Adam Alexander

Alexander's Star
(Equal to a Megaminx with no corners and no centers.)

GloBall

 GloBall [T]
See GloBall variants here.
Kytka (Flower) GloBall

 Kytka (Flower)
A derivative of the Globall. This is a corners-only Megaminx or Pyraminx Crystal, same as Litwin's Kilominx / Meffert's Flower Minx.
Logic Star GloBall

 Logic Star
A derivative of the Globall.
Vega Mate - Raphaël Mouflin

Vega Mate by Raphaël Mouflin Vega Mate by Raphaël Mouflin Vega Mate by Raphaël Mouflin Vega Mate by Raphaël Mouflin

Vega Mate - by Raphaël Mouflin [T]
The Vega Mate is a compound of five tetrahedrons; the base puzzle is a Pentultimate.
Fisher's Golden Dodecahedron

 Tony Fisher's Golden Dodecahedron - Mefferts

Rhombic Dodecahedral Twisties

Since Rhombic Dodecahedra are not regular polyhedrons, they are difficult to classify using the scheme I have employed for the regular polyhedral puzzles.

Face-turning Order 2
FTRD (Rua) - David Pitcher

 The FTRD (Face Turning Rhombic Dodecahedron) aka Rua, by David Pitcher.
FDM (ABS) version of FTRD by Pitcher, with tiles, purchased 1/20/18 for $140 from Chewie's Custom Stickers (Jason Gavril) - see link to FTRD.
Pitcher's announcement of his Shapeways version back in Jan 2012: [T]. David says that though Matt Shepit announced first, in 2008, David designed his in 2003.
Chewie's announcements: [T] [T]
Matt Shepit's Rua from 2008: [T]
"Rua" means "two" in Maori, and refers to the fact that the cuts are less deep compared to the Toru.

In 2009 Eitan Cher designed an FTRD with shallower cut placement (essentially a Rua but with all pieces exposed) (it sold in an auction to Frank Tiex for $614): [T] [Y]

Master FTRD by Eitan Cher: [T] [Y]

Master Rua by Mohammad Badir: [T]

List of other RD puzzles: [T]

Rhombic-18 - David Pitcher

 The Rhombic-18, by David Pitcher. [T] [Y] [S]
A variation of the FTRD, where all faces turn, and all 4-fold corners turn.
Toru (replica) - Sam Jiang 2/2018


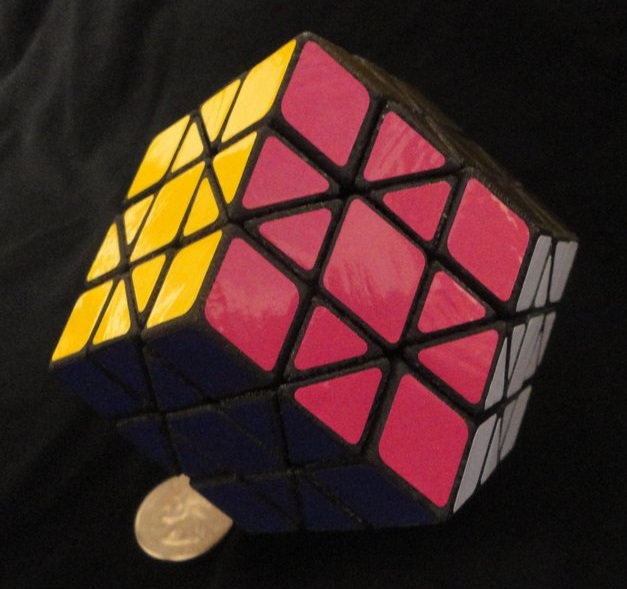
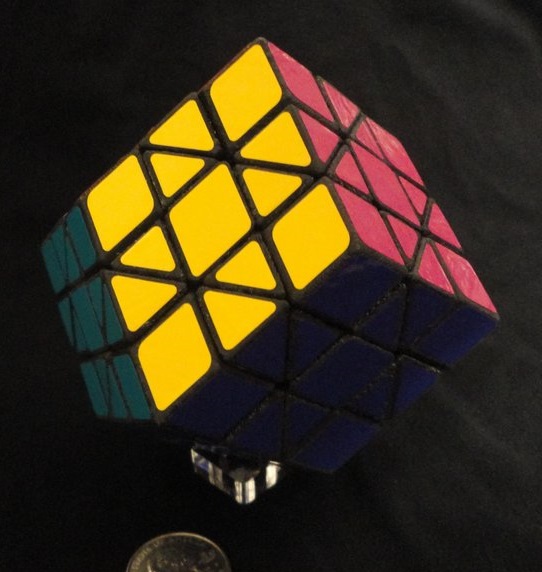
 Toru replica by Sam Jiang [T] [Y]
Matt Shepit's original Toru from 2008: [Y]
This puzzle turns just like the FTRD but is deeper-cut.
"Toru" means "three" in Maori, and refers to the fact that the cuts are deeper compared to the Rua.

A cubic Toru: [T]
Cubic Toru on Shapeways: [S]

Crazy Comet - Oskar van Deventer - Lanlan

 The Crazy Comet, designed by Oskar van Deventer back in Sept. of 2009 [T] and produced by Lanlan in 2017.
Lanlan initially produced this without acknowledging Oskar [T].
This puzzle jumbles.
Vertex-turning Order 2
DRD (Dino Rhombic Dodecahedron) - Drew Cormier

 I bought the Dino-Rhombic Dodecahedron (DRD) DIY from Drew Cormier. This puzzle is a vertex-turning rhombic dodecahedron where all 4-part and 3-part vertices turn. It turns well, but due to a design issue the 3-part corners turn only counter-clockwise.
Rex Rhombic Dodecahedron - William Kretschmer

 This is a Rex Rhombic Dodecahedron (RRD), designed by William Kretschmer. It was announced on the TwistyPuzzles forums, and is available from Will's Shapeways shop. As Will says, the turning is nearly flawless. It's about the same size as the LanLan 4x4x4 RD. This is a great puzzle!
Vertex-turning Order 3
Mini-Mini-Rhombiminx - Eric Johnson

 A Mini Mini Rhombiminx from Eric Johnson.
It's a vertex-turning Rhombic Dodecahedron, but unlike the similar-looking DRD,
the Rhombiminx is order-3 and only the 4-part vertices turn.
It's hand-made using cast custom parts and an Eastsheen mini 2x2x2 core.
Mini Rhombiminx

This puzzle is the same size as the Dino-Rhombic Dodecahedron (DRD) I got from Drew Cormier - here are some comparison photos:

Here is a group shot with various Rhombic Dodecahedra twisty puzzles.

The black Mini-Rhombiminx is in the center. The white Mini-mini Rhombiminx is below it; clockwise from there is a 2x2x2 Rhombic Dodecahedron made by Karl-Heinz Diekmann, a Kite Skewb, a truncated 4x4x4 RD, a Lanlan 4x4x4 RD, a QJ 3x3x3 RD, and the custom DRD.

I received a black Mini Rhombiminx. This is an order-3 vertex-turning rhombic dodecahedron, built around a 2x2x2 using custom parts. (The first Rhombiminx was built around a cut-down 4x4x4.) Every 4-part vertex turns, and there are 3 mutually perpendicular cuts through each square cross-section (i.e. the 2x2x2 cuts).

It is larger than the white Mini-mini Rhombiminx I got a while ago, which is built around a mini-Eastsheen 2x2x2.

Devil's Eye / Evil Eye - Closed

 Moyu Devil's Eye (closed) - invented by Guan Yang
a rhombic dodecahedral form of the cross cube
Devil's Eye / Evil Eye - Open

 Moyu Devil's Eye (open)
Devil's Eye / Evil Eye - Closed, solid Colored pieces

 Moyu Devil's Eye (closed) - with solid colored pieces
Geared
Gear Change - Meffert

 Gear Change pair
Shapemods
Rhombic Dodecahedron Skewb
1.0*108

Rhombic Dodecahedron Skewb
Since the orientation of every piece matters, this is similar to the Skewb Ultimate.

2x2x2 Rhombic Dodecahedron - Karl-Heinz Diekmann

 A 2x2x2 Rhombic Dodecahedron, made by Karl-Heinz Diekmann.
3x3x3 Rhombic Dodecahedron - QJ, LanLan

 Rhombic Dodecahedron (3x3x3) in black (QJ), and white (LanLan)
also truncated version
4x4x4 Rhombic Dodecahedron - LanLan

 Lanlan 4x4x4 Rhombic Dodecahedron
also truncated version
Diamond Cube

 Truncated Rhombic Dodecahedron
This vintage cube-variant is almost a rhombic dodecahedron, except the four-color centers are flat, not pyramidal. The three-color corners are pyramidal.

Icosahedral Twisties

Icosahedral twisties are few and far between - most of them are custom-made. The seminal icosahedral puzzle is the Dogic, but it is out of production and unlikely to come back.

Face-turning Order 1
Jason's Radio Chop (Radiolarian #15) - GB 2.1.5

 Jason Smith completed his series of "Radiolarian" designs, culminating in the deep-cut #15. [T] [Y]
Unfortunately his design does not permit jumbling moves.

Jason created successive versions of the face-turning icosahedron (FTI), starting with a shallow-cut order-2, then moving the cuts deeper and deeper and closer to each other, on his way to where they merge in the deep-cut GB 2.1.5.

  • #1 - Radiolarian I [T]
  • Cornered Radiolarian [T]
  • #2 - Radiolarian II (aka Circo-Radiolarian) [T]
  • #3 - Radiolarian 3 [T]
  • #4 - Radiolarian 4 (equivalent to Eitan's Star) [T]
  • #5 - Cat's Cradle [T]
  • #6 - RadioWeb [T]
  • #7 - Radio Jewel [T]
  • #8 - Radio Jam [T]
  • #9 - Radio Crystal (Jason's Brilic) [T]
  • Jason says #10 and #11 were both failures.
  • #10 - Radio Nova [T]
  • #11 - Radio Star [T]
  • #12 - Radio Nebula [T]
  • #13 - Radio Gem [T]
  • #14 - Radio Fathom [T]
  • #15 - Radio Chop [T] [Y]
Icosahedron Skewb - Tony Fisher

 The closest custom puzzle prior to Jason's Radio Chop is Tony Fisher's mod of a Skewb - the Icosahedron Skewb - from 1996. It has deep cuts - they cut the icosahedron in half - but unfortunately it is not fully cut. [W] [Y]
Face-turning Order 2
Icosaix - Mf8

 Icosaix - mass-produced by Mf8
created by Oskar van Deventer
Jason's Radiolarian II - GB 2.1.1 - Jason Smith, Bob Hearn

 2.1.1 Jason's Radiolarian II [Y]; Bob Hearn also designed and made this form [T]
Radiolarian - Mf8

 Radiolarian - mass-produced by Mf8
Based on Jason's Radiolarian II - GB 2.1.1 - Jason Smith, Bob Hearn
Jason's Radiolarian III - GB 2.1.2 - Jason Smith

 2.1.2 Jason's Radiolarian III [T]
Eitan's Star (DeFTI) - GB 2.1.3 - Eitan Cher / Mf8

 Eitan's (pronounced like "eight - on") Star
Originally designed and 3D printed by Eitan Cher, and named the DeFTI (deeper-cut face-turning icosahedron), a custom version sold for $926. [T]
Mf8 has mass-produced a version and given Eitan credit. [T]
This puzzle jumbles.
AJ Clover Icosahedron

 AJ Clover Icosahedron Black 20 colors
Vertex-turning Order 1
Jason's Icosamate - GB 2.2.6 - Jason Smith

 Jason's Icosamate [T]

Can be built up from a mass-produced Pentultimate as demonstrated by K. Maruyama (kskmaru) [T] [Y]
Maruyama offers the parts on Shapeways (but you need four sets at $50 each).

Icosamate - Mf8 Icosahedron V4
Icosamate - by Mf8
Also known as the Mf8 Icosahedron V4.
A mass-produced version of the order-1 vertex-turning icosahedron.
Originally made by Jason Smith back in 2010.
This puzzle fills an important slot in my twisty zoo, so I couldn't resist,
and ordered the pearl-colored limited edition rather than wait for a black version.
Turning seems fine to me.
I need to decide on a stickering arrangement.
Vertex-turning Order 2
Master Icosamate

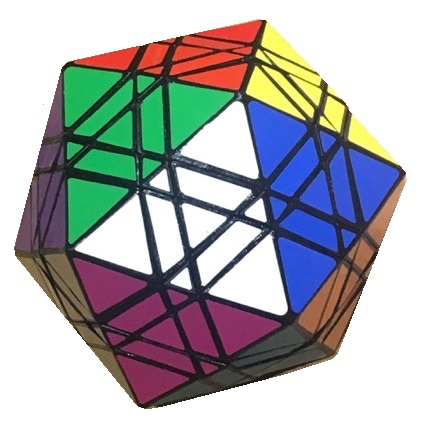
 Master Icosamate - built up from a Master Pentultimate by K. Maruyama (kskmaru) [T] [Y]
Master Icosamate - Mf8 Icosahedron V5
Master Icosamate - Mf8 Icosahedron V5
Tutt's Icosaminx - GB 2.2.1 - Lee Tutt

 Tutt's Icosaminx - GB 2.2.1 - designed by Lee Tutt [T]

In a trade, I obtained an instance hand-cast by Kevin Uhrik.

Icosaminx - GB 2.2.2

 An Icosaminx made by Matt Davis. Originally designed by Jürgen Brandt - a Megaminx mod. [T]
Astrominx - GB 2.2.3 - Eric Vergo

 Astrominx - GB 2.2.3 - Eric Vergo [T] [Y]
"Icosa Minx Mod" - Karl-Heinz Diekmann

 An O2 tipless Dogic made by Karl-Heinz Diekmann [T] [Y]
Kilominx to Icosahedron - Maruyama

 A Kilominx with 3D printed prosthetics, modded into an Icosahedron.
Purchased 1/2018 from "Maruyama" of Japan. [Y] [Y]
Vertex-turning Order 3+
Dogic - GB 2.2.8
2.199*1082 - Zoltan and Robert Vecsei

Dogic (pronounced like "logic")
The tips are not trivial - so this is an order-4 puzzle.
I have an original version (with box), Mefferts I (12 color), II (10 color), and VI (20 color). I don't have Mefferts III (5 color), IV (2 color), or V (2 color).
Jaap's page

Master Tutt's Icosahedron - GB 2.2.14 - Matthew Ray

 Master Tutt's Icosahedron - GB 2.2.14 - Matthew Ray [T] [T]
Olz' DLI - GB 2.2.17 - Ola Jansson

 Olz' DLI (Dual Layer Icosahedron) - GB 2.2.17 - Ola Jansson [T]
Edge-turning Order 1
GB 2.3.1 - 24 Icosahedron

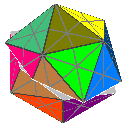
 GB 2.3.1 - 24 Icosahedron - not yet made AFAIK.
Edge-turning Order 2
Icosacopter - GB 2.3.2 - Sharon Avidor and Matthew Ray

 Icosacopter - GB 2.3.2 - by Sharon Avidor and Matthew Ray [T] [T] [Y]
Related
Verypuzzle Clover Icosahedron

Clover Icosahedron Clover Icosahedron

Clover Icosahedron - by Verypuzzle
Tuttminx - Lee Tutt / Verypuzzle

 Tuttminx - designed and prototyped by Lee Tutt in 2005 [T]
Produced by Leslie Le [T] [W]
The Tuttminx is a 32-sided truncated icosahedron.
Tuttminx Classic - Verypuzzle

 Leslie Le has also produced the Tuttminx Classic. [T]   www.verypuzzle.com
Void Tuttminx - Verypuzzle

 Void Tuttminx www.verypuzzle.com
Superstar - Verypuzzle

 Superstar www.verypuzzle.com
Lovebird - Verypuzzle

 Lovebird www.verypuzzle.com
VTI (Void Truncated Icosi-dodecahedron) - Verypuzzle

 VTI (Void Truncated Icosi-dodecahedron) www.verypuzzle.com

Spheres, Eggs, and Pucks

Mozaika
6.27*1049 - Rudolf Destics

Mozaika

The three interlocking equatorial bands of square tiles can be moved around the sphere. In addition, you can rotate a group of four triangular "corner" pieces with the associated nine squares, in increments of 90 degrees.

Impossiball
2.36*1025 - William O. Gustafson
Wolfgang Kuppers

Impossiball
(Equal to a Megaminx with no edges and no centers.)

Traiphum's Megaminx Ball

Traiphum's Megaminx Ball
Produced by Calvin Fan at Hknowstore.

Thomasball

 The Thomasball is essentially the same as the Impossiball, but with a different mechanism.
Ball.B
7.12*1040

The Ball.B - from Poland. This shape - a spherical Megaminx (aka Ballminx) - was first explored by Jürgen Brandt.

The version with dots is like an edges-only Megaminx, since for this version the corner orientations don't matter.

The version with flags is equal to the Megaminx but with face centers orientation visible - i.e. a "Super-Megaminx." That has 2.5*1076 positions.

Masterball
4.1*1020 - Dr. Geza Gyovai - patent 4856786

Masterball (Geomaster, aka Rainbow version), Duo B&W, Dragon, Circus, Soccer

See other versions at Les Casse-Tete de Chantal

Marusenko Sphere

 Marusenko Spheres
Dioctipoid

 Dioctipoid 1 and 2
www.dioctipoid.com

These are face-turning octahedra in spherical form.

Twistball



4 Color and Flower Ball versions

Twist Ball

The Twistball is a spherical Dino Cube, but where the corners are visible. It is available with many different colorings/patterns. The 4-Color version is very simple. The Flower Ball requires all pieces to be correctly placed and oriented, so is slightly more difficult. As with the Dino, both can be solved intuitively without algorithms.

Geert Hellings wrote up a nice post on the Tp forums about the history of this puzzle.

Intellect Ball

 Intellect Ball
9 cm (handy) and 13 cm (large!) versions.
3x3x3 Sphere

 A standard 3x3x3 cube in spherical form. From various vendors, in various sizes.
Rubik's World 3x3x3 Sphere
2.7*1021 - Erno Rubik

Rubik's World

Rubik's World 2x2x2 Sphere

 Rubik's World 2x2x2 Sphere
Finder Ball

 The Finder Ball was available in various colors/patterns. It is a 2x2x2 sphere. My version is a globe, in Spanish.
Hungarian Zodiac Machball (2x2x2 Sphere)

 A vintage Hungarian Zodiac Machball.
Gundam Seed Haro Ball (2x2x2 Sphere)

 Gundam Seed Haro Ball - a vintage collectible 2x2x2 twisty puzzle, made in China and issued circa 2003 by PALBOX of Japan. [T]
This is the pink version, though it looks orange on the front because of exposure to sunlight over time.
D Ball

 The D Ball was available in various colors/patterns. It is a 2x2x2 sphere.
Venus Dreamball

 The Dreamball was available in various colors/patterns. It is a 2x2x2 sphere. My copy is a Venus Ball.
Quarks

 Quarks is from Fourier Idea, Inc.
It is a hollow 2x2x2 sphere.
Magic K-Ball

 The K-Ball is a 2x2x2 sphere. It was offered in various colorings/patterns.
Spherical Skewb
2160 for the 4-color

Various Skewb-core balls including a Mefferts Beach Ball (4 color) and a Beijing Olympics ball

Skewb Egg - Tony Fisher - Meffert

 A white Skewb Egg from Meffert, designed by Tony Fisher.
Morph Egg - Adam Cowan - Meffert

 Morph Egg
Produced by Meffert, designed by Adam Cowan. Based on a 3x3x3, but the subtle curves make this mod surprisingly difficult to solve!
2x2x2 Egg - Meffert

 2x2x2 Egg - Metalized Blue - Meffert
3x3x3 Egg - Meffert

 3x3x3 Egg - Metalized Blue version - issued by Meffert
Gear Egg

 Keychain Gear Egg
Brainbow
623,760

Brainbow
Jaap's page

Rubik's Cheese (Sajt)
96

Rubik's Cheese (Sajt)
Hungarian patent, 9 November 1980, HU 2679

Kep Korong

 Kep Korong - a rare vintage twisty puzzle invented by András Végh, a Hungarian physicist.
Patent HU 184418, filed on 01 April 1981, granted on 30 June 1987.
Ayi's 3-Layer Cheese

 Ayi's 3-Layer Cheese
Canadian Barrel

 Canadian Barrel designed and 3D printed by Tom van der Zanden
A limited-edition Ottawa souvenir Purchased from Tom at IPP35
Works like the Cheese.
Gear Ball

 Gear Ball - designed by Oskar van Deventer, produced by Meffert

Dihedral Twisties

This section contains dihedral puzzles - puzzles whose halves can move relative to each other, usually along only one cut plane, and permit the exchange of pieces between them. Their shapes usually aren't convex polyhedra, nor simple spheres, cylinders, or pucks.

Quartet

 The Quartet from the Shapeways shop of "RubixFreakGreg" -- designed by "Lykwid" [T], the Quartet is a square version of the triangular Grimace made by Smaz.
2-Layer Grimace

 2-layer Grimace
3-Layer Grimace

 3-layer Grimace
Smart Alex
6*1020

Smart Alex
Dumitru A. Pop, patent on 26 May 1992
Jaap's page
Rubik's UFO
4*107 - Erno Rubik

Rubik's UFO
Original in gray, newer version in green.

Logi-VIP
2.7*1025 - 1982 Logitoy AG, Austria - Hubert Petutsching
Patent WO8101638

Logi-VIP

Bulgarian Barrel

 The Bulgarian Barrel
Olidjus

 Olidjus - a rare vintage original twisty from Russia
Square 1
4.36*1011 - Dr. Vojtech Kopsky

Square 1

90 possible shapes

Square 2

 Square 2
First designed by Dave Litwin, "Jake," and "Noda" back in 2003 [T], then mass-produced [T].
Super Square 1
1.19*1022

Super Square 1 (4-layer)
Produced by cube4you.
Watch a video.

Super Square 1 Star Mod

 A Super-Square-1 Star mod - Brett made it in all white then I swapped in the black pieces.
You can find on-line [dis]assembly instructions here.
Rainbow Nautilus - Selkirk - Meffert

 The Rainbow Nautilus, designed by Tim Selkirk [T] and mass-produced by Meffert.
Octo Bracelet
3.7*1018 (?)

Octo Bracelet

Sando Ring
4.97*1014

Sando Ring
(aka King Ring)

Tricky Disky
2.1*1013

Tricky Disky
Jaap's page

Hungarian UFO
2.1*1013

Hungarian UFO

Brainball
2*1012

Brainball
Andreas Unsicker
Jaap's page

Sphere XYZ
3.37*1011

Sphere XYZ
Offered by Lori Powers and Adam Giemek,
and LA1 Products

Buzzle Ball

 Buzzle Ball (mass produced)
Netblock UFO
2.0*108 = 200,121,075

Netblock UFO
Wai K. Chan

Gerdig UFO
130,040

Gerdig UFO
Gerhard Huncaga
Jaap's page

Saturn - MagNif
5040

Saturn
Jaap's page

Clever Disk

 Clever Disk
Turbo Mind Twister

 Turbo Mind Twister
Snow Mystery

 Snow Mystery
TrueChallenge

 TrueChallenge - a dihedral puzzle where one must match the magnetic segments

Strange Twisties

This section is a catch-all for other twisty puzzles that aren't easily categorized above. In no particular order.

Roundy

The Roundy appeared in various configurations. They included (but weren't necessarily limited to):

3-leaf 3-color (2880 states), 3-leaf 6-color (23040 states), 4-leaf 4-color (40320 states)

Group shot:

 Roundy - Fritz Gruber 12/7/93 patent 5267731

Roundy 4-leaf 4-color version purchased at IPP28 in Prague.

Jaap's page

DaYan Gem II

 The DaYan Gem II is a truncated cube where faces of the cube and vertices of the cuboctahedron rotate.
DaYan Gem III

 Here is a Limited Edition Blue DaYan Gem III. [T]
It is a shallow-truncated octahedron where the vertices and faces turn. Independently designed by Daqing Bao, also appeared as the custom "Concept 11." [T] Shown compared to the DaYan Gem, which is a truncated edge-turning octahedron.
DaYan Gem IV Deepcut

 The DaYan Gem IV resembles the Gem III, but here the 4-fold faces (the trancated octahedron tips) do not turn. Instead, the puzzle is deep-cut. Every hexagonal face turns, but the layer below and parallel to each hexagonal face also turns.
DaYan Gem V

 The DaYan Gem V.
DaYan Gem VI

 The DaYan Gem VI.
DaYan Gem VII

 The DaYan Gem VII.
DaYan Gem VIII

 The DaYan Gem VIII.
Floppy 2x3x3 - Oskar van Deventer

 I took advantage of a special offer at Shapeways for a dyed, assembled, and stickered Floppy 2x3x3 designed by Oskar van Deventer.
More Madness - Oskar van Deventer

 Prolific puzzle designer Oskar van Deventer [S] attended IPP 31 in Berlin, and I purchased his More Madness, which he was kind enough to sign for me. No-one has yet devised a comprehensive solution strategy for this puzzle. More Madness was announced and discussed on the TwistyPuzzles forum. It is based on the geometry of the triangular di-pyramid. Initially, each of the triangular faces turns. This puzzle has "overhang bandaging" - occasionally a piece juts out such that it blocks a twist that would otherwise be OK. Every move jumbles.
Treasure Chest Cube - Oskar van Deventer - Mefferts

I received a black Treasure Chest cube from Mefferts.
This hollow, opening cube was designed by Oskar van Deventer - he called it the Gift Cube. [T]
DaYan Pentahedron 3x3

 DaYan Pentahedron 3x3
I have the "special" standard 3-layer (non-circle/crazy) version. Also available: special standard 5-layer, special super 5-layer, and a set of eight different crazy/circle versions named after planets: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune.
Child's Play - Eric Vergo

 Child's Play by Eric Vergo [T] [S] [Y]

This is Eric's first copy!

Two 2x2x2 cubes with shapes on each face reminiscent of the shapes in a child's shape sorter puzzle/toy - hence the name. One cube has the shapes embossed into the facelets, the other has raised shapes. The objective is to solve both cubes such that every face on the cube with raised shapes can be fit into a corresponding face on the cube with embossed shapes. Difficult, especially if you don't know what the shape arrangements are supposed to be! The colored layers aren't necessary, but have been added to simplify the challenge somewhat.

Mini Mixup Cube - Mike Armbrust

 A Mini Mixup Cube by "PuzzleMaster6262" (Mike Armbrust) [T] [S] (also see a version by Oskar van Deventer [S] )

The idea of a 3x3x3 cube which is able to interchange edges and centers via 45 degree turns of its middle slices seems to have originated with Sergey Makarov back in 1984. [T]

Mixup Cube

 The Mixup Cube, designed by Oskar and mass-produced by WitEden.
Octo-Star Cube - David Pitcher

 The Octo-Star Cube, designed by David Pitcher and mass-produced by Calvin Fan.
It has been described as an unbandaged Bermuda Cube.
X Cube

 The X-Cube from Calvin's Puzzles.
Cross Cube

 The Cross Cube from Calvin's Puzzles.
Time Machine - Smaz

 The Time Machine - a beautiful twisty puzzle designed, made, and stickered by Smaz. [T] [T] [T]
A 2x2x2 where each face has a "dial" of 12 movable segments. Similar to the Square-1 Cross Cube. [T]
Wheel of Wisdom

 The Wheel of Wisdom by DaYan
Wheel of Time

 Moyu Wheel of Time black
A nice shapemod of a Cross Cube.
Moyu Fisher Yileng Time Wheel stickerless

 Moyu Fisher Yileng
Time Wheel stickerless
Wormhole I Cube - WitEden

 A Wormhole I Cube by WitEden

Several other variants are available.

ShengShou Cubes

 A set of ShengShou Cubes, and the "Circle Ball Cube"
Dual Rings

 Dual Rings, designed by Oskar van Deventer and Bram Cohen,
manufactured by Hanayama.
Hog Wild Double Disk

 Double Disk from Hog Wild LLC of Portland OR
Hog Wild Double Think Binary Ring Puzzle

 The Double Think Binary Ring Puzzle from Hog Wild LLC of Portland OR

Three layers - in the top and bottom layers, the pairs of interlinked rings turn independently, allowing segments to be mixed between them.
In addition, each ring has twelve segments that can be flipped to mix between the layers -
such a move also exchanges inside and outside segments from the middle layer.
The segments flip smoothly but it is somewhat difficult to rotate the rings.

Q-Borg

 Q-Borg - by Auldey
Bubbloid 4x4x5

 Bubbloid 4x4x5 - designed by Carl Hoff. Carl Hoff has created a vertex-turning cuboid he calls the Bubbloid, based on some ideas by Anthony Villaveiran (boublez). [T] [T]
Produced by Calvin's Puzzles
I got a limited edition blue.
Bubbloid 4x5x5

 Bubbloid 4x5x5 - designed by Carl Hoff,
produced by Calvin's Puzzles
I got a limited edition blue.
Clover Cube

 Clover Cube - Verypuzzle
Solutions available on YouTube - e.g. [Y], and [Y1], [Y2], [Y3]
Pentacle Cube

 Pentacle Cube - QiYi - Yukang Wu.
Bagua Cube

 Bagua Cube - DaYan
Coin Cube


 Coin Cube - QiYi
Also known as the "Copper Coin" or "Ancient Coin" cube.
I got the stickerless version.
Each face can rotate in place, moving its four oval-shaped pieces. Aligning the ovals properly at each corner will allow vertex twists, which move the three oval pieces surrounding the corner.
An easy-to-solve puzzle that does not require algorithms. At a puzzle gathering, several non-twisty puzzlers were able to solve this cube intuitively.
Evil Seed

 Evil Seed - designed by Vladi Delimollov - mass-produced by Calvin's Puzzles
Slim Gigaminx

 Slim Gigaminx - Evgeniy Grigoriev
CaTSuP

 CaTSuP (Corner-Turning Square Pyramid - designed by Braden [T], 3D printed by Jason Gavril (Chewie)
A Corner-Turning Square Pyramid
Konrad posted solving tips on the TP Forums.

Unusual Permutation Puzzles

Here are other unusual and interesting takes on the permutation puzzle...


The Planets puzzle consists of four spheres arranged in a tetrahedron within a frame. The spheres have various craters in them and are contrived to interlock so as to only permit certain rotations depending on where the craters are at any moment. Rotate the spheres so that each side of the tetrahedron is a uniform color.
Cmetrick is from eLogIQ. There are 6.9*109 possible positions. Jaap's page eLogIQ has also released the Cmetrick Mini.
I got an Enigma from Norman Sandfield at the 2005 NYPP. He said the reason they've been so hard to find is that the firm that makes them only sells them in bulk for advertising promos. However, recently I've seen a color version for sale at the Puzzle-Shop. I found a second version, a promo for the University of Connecticut Health Center, on auction. [Jaap's Enigma page]

This is a variant of the Enigma, a French puzzle called "Combinescion."
This is the Spectra, by Eng's I.Q. Co. Ltd. 1987. 3072 positions. Jaap's page
Hoppa Gula

Rubik's Clock
Rubik's Rabbits
Rubik's Pen by Ideal from 1982.


I found this puzzle, called "Boomdas" ブームダス, many years ago but I cannot recall the circumstances. I used to travel to Tokyo on business in the 1980's and found many interesting puzzles in Japanese department stores, but I may have acquired it in a private transaction with another long-time collector.

The key feature of the puzzle is that it implements a sliding piece puzzle but doesn't need a tray - the pieces interlock along their edges and can slide relative to each other while remaining attached. Boomdas is a two-dimensional/planar example; the concept has appeared in three-dimensional cubic forms with the Muto Cube - another puzzle I found in Japan in the 80's - and the Bishop Cubes, a more recent puzzle (but still a few years old). The interlock geometries of the puzzles are all slightly different.

Oskar van Deventer learned of Boomdas and over the years has created a few variants he has 3D printed - he didn't like the fact that in the original, pieces can be completely detached which allows one to cheat. Oskar added features to prevent pieces from being completely detached.

Here is a link to his OsDas 3x2 and and his 3x3 version. The 3x3 OsDas is available at his Shapeways shop, at $850. The blurb has broken links to my old Comcast website. Here is a link to Oskar's video about his OsDas 4x4.

There has been some recent discussion in various puzzle forums about one of Oskar's variants, and I suspect this accounts for the renewed interest in the original puzzle - the latest is called Segerdas.

Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle Boomdas puzzle

A set of Bishop Cubes. Their website, bishopcubes.com, is defunct.

The Virus
Kinato Hex Pro (Warning: website requires Chinese character set) and Kinato Hex 7
Orbik

Kabalabda Ball
See U.S. Design Patent D283523 awarded to Margit C. Balint in Apr. 1986. 		 
Magellan
This turns out to be based on the Four-Color Map Theorem. The objective is to ensure that all adjacent areas contain different colors on their wheels, on both sides of the puzzle at once.
I have a white version, and a black one in its package.
Labyrint

Gear Up - designed by Oskar van Deventer
made by George Miller
Eggcentric - designed by Oskar van Deventer
Writer's Block - designed by Oskar van Deventer, purchased from Bits and Pieces.
Produced by RecentToys.
Use an included "key" to find a set of moves that extends all the pens, allowing the box to be opened and the pens to be reset. Reminds me of "Lights Out."

This is the Jugo Flower, made from metal, from William Strijbos. The Jugo Flower (aka Yugo Flower or Game Jugo) is one of the most rare twisty puzzles - I have read that only seven prototypes were made. You can see examples of the original plastic versions at Hendrik Haak's website. Wil has had the puzzle reproduced in metal. The fifteen petals can each be flipped over around the long axis. There are four marks on the top of the aluminum hub, and only those four petals positioned at the marks are able to flip, simultaneously. All the petals can be rotated around the hub, provided they are properly aligned (the mechanism is somewhat "catchy"), and a new set of four petals can be positioned at the marks. The goal is to scramble the petals, then restore them to all face-up. This puzzle is similar in principle to "Lights Out."
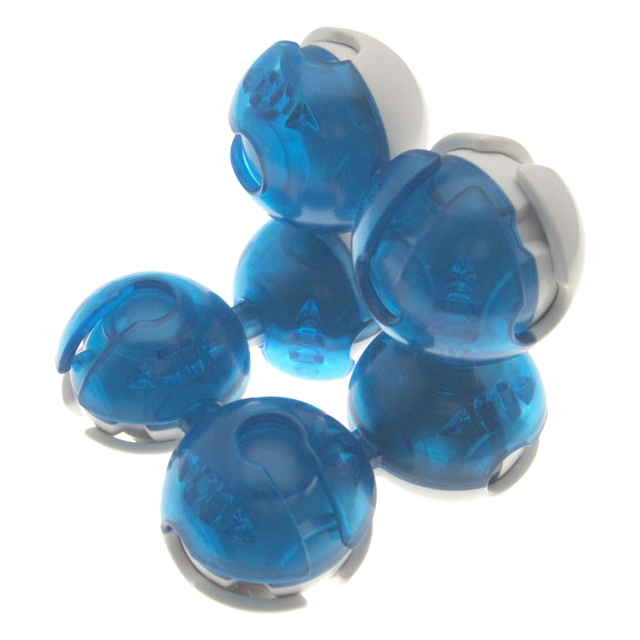
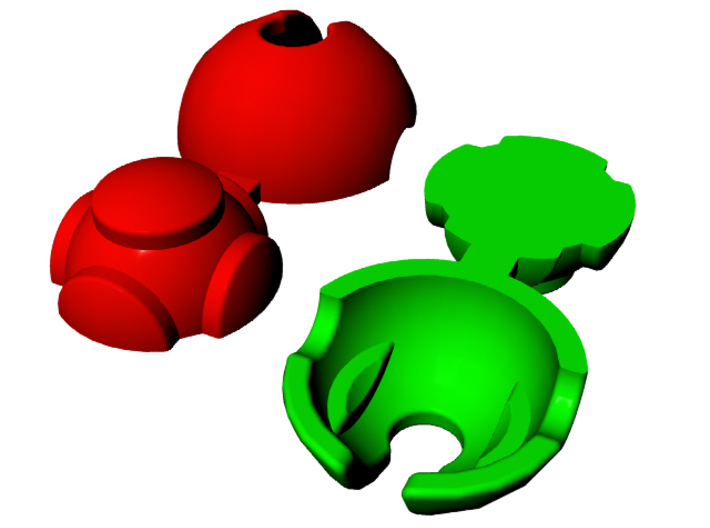
Bram's Magic Bram's Magic Bram's Magic Bram's Magic
Bram's Magic - designed by Bram Cohen and Oskar van Deventer

Gear Shift - Bepuzzled
Purchased online off Amazon.

I have had a Columbus' Egg puzzle since I was a kid. U.S. Patent 4489944 - Hatakeyama 1984. I also still have the instructions, though the packaging is long gone. I have found very few references to it on the web (TwistyPuzzles has a version with different branding listed with no info) and have had to wade through a lot of unrelated material because of the name. The instructions say it was issued by HirschCo at 2633 Greenleaf Ave. Elk Grove Village, IL 60007.

To scramble the puzzle, when all 5 red segments are showing through the window, turn the egg small end down so that an internal weight moves to the small end. Push the slide one or two positions and turn the base several times. To solve, get the egg to stand upright on its large end. You have to line up all red segments in the window again. Each of the 5 cylinders has 10 segments one of which is red. So there are 105=100,000 possible states. The 3-position slider controls which cylinders turn when you turn the egg's base. The instructions say all turns should be clockwise. From my experience, sometimes the cylinders "misfire" or skip. Here is a movement chart from the instructions - the slider position is either up (towards the small end), in the middle, or down (towards the large end). Number the cylinders 1-5 starting from the small end.

Slider
Position		 Cylinders
which move
Down1, 4, 5
Middle3, 5
Up2, 4, 5

3-Dimensional Sliding Piece Puzzles

There are many 3-dimensional sliding piece (or sliding block) puzzles. Some consist of a framework or container inside of which are movable colored cubes. In some, there are moving marbles or beads instead of blocks, and in some cases the frame itself can be re-configured. Usually there is a single "hole" which can be thought of as moving around. Sometimes, however, the moving frame accomplishes the permutations of the piece positions and no hole is needed. In yet another sub-category, there are flat plates which can overlay each other. Still another sub-category accomplishes permutation using pieces as segments of interlocking rotating disks.

Movable Gap, Rigid Frame

Bloxbox designed by Piet Hein and issued by Hubley in 1972.
I found a second clean example, in its original (albeit damaged) package.
The Bloxbox is notable since the design by Piet Hein is one of the first examples of sliding cubes in a cube.
(The first U.S. patent, 416344, for a puzzle like this was awarded to Charles Rice in 1889.)

Pepsi Can
Start with an idea as simple as mapping a 15-like puzzle onto a cylinder. This puzzle has advertised several popular drinks.
Billiards 9-Ball
created by Joshua Frankel
3,628,800 positions
Jaap's page
Massage Ball
Otto Wu
patent on 14 Feb 1995
6.1*1019 positions
Jaap's page

Vadasz Cube (2x2x2 and 3x3x3 versions)
(Also 4^3, which I don't have.)
Minus Cube (Russian)
Varikon black

Peter's Black Hole
5.4*1027 positions
Jaap's page

Twistypuzzles.com has an article by Ad van der Schagt titled "The History of Sliding Block Puzzles Before Peter's Black Hole" (PDF).


Clark's Cube
I-Qube

This is called the "Switch" or the "Knox Transposition Puzzle." It was issued by Mag-Nif in 1970 and also appears in their "Game Chest" set. The pegs slide in channels in the base. The object of the game is to exchange the sets of colored pegs in 24 moves or less. This actually borders on a non-jumping (exchange-only) type of Peg Solitaire.
Crossteaser
2.7*1011 positions
[Crossteaser home page]

Inversion
Mad Marbles by Lakeside (2 instances)
Magic Jack

Tumbler - van Deventer
Pionir Cube
Panex
Panex Puzzle resources page at Baxterweb
Play a level-4 version online at cheesygames.com.

A cross between the Pionir Cube and Munroe's Marbles, from China.
Orbo, by Popular Playthings; and an Asian clone - the Magic Rainbow Ball by Yong Jun
Rainbow Black Hole

? (Hungarian barrel)
Diamond Bob's Billiards Eight Ball, and Diamond Bob's Diamond 8
Rubik's Brain Racker

Bolaris
Designed by Hannu Hjerppe of Finland - website at www.bolaris.fi. Purchased at IPP28 in Prague.
Cubedron and Cybedron
Pantazis Houlis at Mindstrat Puzzles has invented a series of what he calls "Gravity Puzzles." These are edge-matching puzzles encloszed in transparent spheres, where the pieces must be tilted into position so that patterns along the edges match, and a piece flips as it moves from one position to another.

Equal-7 - issued by Recent Toys
Invented by Vladimir Krasnoukhov
Tilt the cube to slide the dice - four successively harder objectives - make the total on all sides: 10, 11, 12, 7.
Pionir Pyramid, designed and exchanged at IPP32 by Roxanne Wong; made by Mf8
A vintage sliding piece puzzle in the shape of a bottle of Glenlivet Scotch.
Movable Gap, Movable Frame

Mind Twister aka Wisdom Ball
Yang Ju-Hsun
1 June 1993
1.7*1075 positions
Jaap's page
Saturn - LD Belgium
white and black versions
Tomy Great Gears
1.46*1020 positions
Jaap's page

This is called Entrapment. There are also some newer "clones" available. The clear plastic on the old ones is yellowed with age.
Atomic Chaos
Christoph Hausammann
2.1*1012 positions
Jaap's page
Pakovalec
aka Xylinder
1.3*1010 positions
Jaap's page

Missing Link
and the rarer Limited Edition
Marvin Glass & Associates
8.2*1010 positions
Whip-it
5.7*108 positions (for the 3)
Jaap's page
Bola RUVI (Whip-it Ball)

Ivory Tower and Babylon Tower
both 6 rows x 6 cols
1.9*1040 positions
Jaap's page
Varikon
4x4, 5x4 and 7x7
1.4*1014 positions
Jaap's page
Backspin
and a clone by Jaru
Ferdinand Lammertink
6.4*1028 positions
Jaap's page

Tomy and Milton Bradley Rack 'Em Up
Mizunuma Masanori and Watanabe Hiroyuki 1984
6.3*107 positions
Tomy Row By Row
Mizunuma Masanori
and Watanabe Hiroyuki
13 Nov 1984
2.8*1031 positions
Jaap's page
SpongeBob Puzzlepants
10,080 positions

Sherman head - McDonalds premium
Bognar's Brainteaser Smile
produced by Huch!

Aztec Ghost Tower - True Genius


Russian Festival Flower
A vintage 3D sliding puzzle
I have examples of the 1-petal, 5-petal, 6-petal, and 12-petal versions.

Touchdown
Calendar/Bank
Heartache - Kohner

Spinzillion - like the classic Ten Billion Barrel
Da Vinci's Mona Lisa Codebreaker, Twisted Mind - another version, using numbers, and with a transparent case, and Twist O Mania

Double Sliding - Dario Uri 		Here are three different 3-D sliding piece puzzles by Doug Engel: Blocked Barrel 15, Barrel Slide 121, and Barrel Shuttle 11.


The Mini and Braille Eni Puzzles
Capzule
Instant Insanity II - by Winning Moves.
This reminds me of the Pakovalec (aka Xylinder).
No Gap, Rigid Frame (Interlocking Orbits)

Equator, and Hungarian Globe
1.1*1025 positions
Jaap's page
Hungarian Rings
Endre Pap
7.5*1019 positions
Jaap's page
Magic 8
Race War Puzzle Between Gold & Silver
Race War Puzzle Between Gold & Silver - a vintage sliding piece puzzle
of the "No Gap, Rigid Frame (Interlocking Orbits)" type.
See U.S. Patent 507215 - Churchill 1893.
The "war between gold and silver" referred to here was a major political issue regarding currency in late 19th-century America.
See the Wikipedia article on Free Silver.
(Another puzzle named after the same issue is the "16-to-1" shuttle maze.)
I found only the board - no pieces (the patent shows 22 pieces in each ring, with two shared between the rings at the crossing points),
but I had some time ago saved internet photos showing a cover and some pieces...


Rubik's Rings
1.9*1014 positions
Jaap's page
a source
Circle Puzzle
369,600
[Jaap's page]
Rotascope
Raoul Henrique Raba 1982
9.1*107 positions
I obtained this Rotascope which is a souvenir of the sixth IPP at Jerry Slocum's house. The front contains invitation text and Jerry's home address and phone number, which I don't want to display here. This is a picture of the back - not very puzzling without a pattern to scramble.


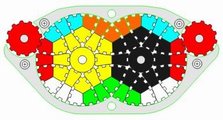
Tsukuda Magic Puzzle
(Turnstile)
Douglas Engel
6.3*109 positions
Jaap's page


Mandorla

Lotica

Turn Push
Whirligig

Mad Triad
3.1*1045
(symbols matter)
Jaap's Page
Handy Mad Triad
8.3*1023 positions
Jaap's page
Rubik's Shells
4.7*1014 positions
Jaap's page

Cmetrick Too
There are colored disks riding in "craters" in spheres embedded in the frame. The spheres rotate and can exchange disks.
Cmetrick Too Hard
In this more difficult version, the centers of the disks are colored, too.
The Arusloky Puzzle

Twiddler Double Dilemma - designed by Wilfried Braun

Twiddler Triple Temptation
 
3-layer and 4-layer Leesho (Liso)
Hungarian Olympic Rings
Twinspin - Brainwright
Thanks, Alison!
This puzzle is called Moeraki, a name chosen since the shape of its pieces is reminiscent of a formation of spherical boulders found in New Zealand.

It was designed by Kasimir Landowski and won an IENA gold medal at the 2008 Nuremberg Trade Fair. You can read about the history of the puzzles and order them online at the Casland Games website. Various virtual examples are available at the website and each physical puzzle includes a disk offering some virtual puzzles.

Moeraki is a type of sliding piece puzzle, which I would categorize as of the No Gap, Rigid Frame (Interlocking Orbits) variety. Moeraki No. 3, the one I have, has a square tray and two interlocking oval tracks of pieces in five colors. Moeraki No. 4 has a triangular tray and three interlocking circular tracks of pieces in four colors.

I received my No. 3 as a gift at IPP32, on the condition that I review it. Normally, I don't blog or review puzzles per se, but I accepted it since I had planned on buying one anyway. A policy of mine in general is to try not to say anything if I don't have something nice to say (in print, at least). I don't always succeed in keeping to my policy, but happily I will be in no danger here since I honestly like the Moeraki puzzle.

The concept of a set of markers riding in interlocking circular or oval tracks, which can be mixed by alternate rotations of the groups of pieces in the different tracks, is certainly not new. An example called "Race War Puzzle Between Gold & Silver" designed by William Churchill was awarded U.S. patent 507215 in October of 1893. More recent examples include the Hungarian Rings puzzle by Endre Pap et al (EP0050755) , and the Magic 8. On the Casland website it is mentioned that Ivan Moskovich also received a patent for a similar idea in 1979 (see U.S. patent 4509756), and is now collaborating with Landowski. Original concept or not, the Moeraki puzzle stands out as a very nice implementation and is probably among the most user-friendly of this class of puzzles in my collection.

You can find analysis and solutions of the puzzles at Jaap's Puzzle Page. Jaap gives the total number of possible arrangements for No. 3 as 3,969,069,923,590,200, which, surprisingly, is still larger than the U.S. national debt. Jaap notes that any two diametrically opposed beads will always remain diametrically opposed no matter what moves you make, which I find non-obvious on initial inspection, and fascinating.

Dieter Gebhardt has also published some analysis about this type of puzzle. Dieter's article "Rotational Puzzles with Two Tracks and Two Intersections" can be found in the March 2002 issue #57 of the journal of Cubism For Fun (CFF). Dieter's article supplies a notation convention and a general theoretical basis for deducing useful move sequences, and would be of interest to one attempting to gain a more than superficial understanding of such puzzles, although it deals with types of only two intersections.

These puzzles may appear to be intrinsically simpler than puzzles such as Rubik's Cube and its ilk, and in truth it is possible to attack them without extensive knowledge or analysis of solution procedures or "operators." And, as with twisty puzzles in general, the large number of possible states is not a reliable indicator of difficulty. However, it should be noted that some piece swaps may require upwards of 100 moves to solve, so patience and perseverance will definitely be assets to the recipient of these puzzles. At his website, Diniar Namdarian gives instructions for accomplishing a last swap of two pieces.

When I played with mine, I found the very first challenge to be simply opening the package! The puzzle ships in a cardboard box, which contains a clear plastic case for the puzzle, secured by four clips. A clip can be removed by prying its rounded end away from the case, but the force required makes one leery of breaking something. The puzzle is 135mm square and about 15mm thick. Production values are high - the plastic is good quality and brightly colored. A thoughtful touch is a removable block on the perimeter of the base, which will allow you to extract the sliding pieces from the puzzle in order to effect a brute-force restoration of the solved state, should you deem that necessary. The case also holds a CD-ROM containing additional puzzle software.

For me, assuming one enjoys this class of puzzle, two criteria determine whether a puzzle of this type succeeds or fails as a mechanical puzzle worth playing. First, do the pieces remain securely in their tracks? I have had copies of Hungarian-Rings style puzzles where the beads just fell out. I can report that the puzzle is well-engineered and well-built, and the Moeraki beads will not come out by accident. Second, is it easy to rotate the pieces along their tracks, preferably while holding the puzzle in two hands and using only one's thumbs to slide the pieces? Here I can also give the Moeraki a good grade. As with all interlocking-orbit type puzzles, the orbits must be properly aligned so that the pieces do not catch and impede movement. Out of the box, the movement of the Moeraki beads is somewhat stiff, but a benefit is that the tracks of beads do not tend to overshoot on a move, and a simple tilt of the puzzle will not cause unwanted movement. I gave it a shot of CRC Industrial Food-Grade Silicone spray and now the action is silky smooth!

I think the Moeraki would make good Christmas presents for the puzzler in your life (or for yourself). See what other puzzlers have had to say about the Moeraki puzzles here, here, and here.

Arancia Meccanica
Arancia Meccanica - a vintage 3D sliding piece puzzle [T]

The V-Sphere was invented by George Xronopoulos and released in mid 2017. It is a sliding piece type puzzle encircled by three mutually orthogonal pairs of rings in which square sliding tiles ride, fitting the surface of the sphere. There are eight colors - each tile is molded of one color, and there are eight triangular sections fixed around the sphere between the rings. The colors of these triangular regions define the goal state - move the tiles so they surround their correspondingly colored triangle.

In its default configuration the puzzle contains a single empty space - it is a member of the class I call "moving gap, rigid frame" or MGRF. However, one can obtain an extra (dark blue) tile and fill in this space - the puzzle then becomes a "no gap, rigid frame (interlocking orbits)" NGRF type - and most puzzlers agree this is the preferred configuration as it increases the difficulty. This latter category contains the spherical forebears the Equator, the Hungarian Globe, and the Arancia Meccanica - but each has only a single row of tiles in each orthogonal direction. Perhaps the earliest example of an interlocking orbits type puzzle - albeit non-spherical - is the "Race War Between Gold & Silver" puzzle of 1893.

The V-Sphere is a nicely packaged, well-made and colorful example of an established puzzle category, and ups the complexity ante with its side-by-side rows of tiles. (This innovation is not unique, however, as a Russian puzzle dating from 1986 or earlier implemented dual rows of tiles - see this entry at the TwistyPuzzles Museum.) I find the selection of colors attractive, and the size and weight fit my hands well. The sliding action of the tiles is smooth, and the "clickiness" serves to prevent overshoots. The ability to easily convert it from a relatively easy MGRF to a more difficult NGRF type is an added bonus. According to sources, the puzzle was originally designed without the gap, but was released with the gap in order to reduce the difficulty level. Inserting the missing tile is simple, and the rotations of full rings of tiles works well.

No Gap, Movable Frame

Topspin
Ferdinand Lammertink
2.4*1018 positions
Jaap's page
Trillion - red, black
Gunpei Yokoi
1.0*109 positions
Jaap's page
Nintendo Ten Billion Barrel
and Club Nintendo Star Barrel
Gunpei Yokoi
2.7*1014 positions
Solution site here.
Tom's Turnstile - Cutrofello - Brainwright
Tom's Turnstile - designed by Tom Cutrofello, issued by Brainwright
A nice, substantial brass sliding-piece puzzle -
I categorize as of the "No Gap, Movable Frame" type.
Thanks, Alison!

I have seen this design from several places. I believe it has been called "Sortospherical."
The Orb[-it]
Christopher C. Wiggs
and Christopher J. Taylor
7.4*1028 positions
Jaap's page
Astrolabacus
John D. Harris
Pat. 8 Jul 1997
3.6*1016 positions
Jaap's page

Bananacus - Brainwright
Thanks, Alison!
Gripple
Murray J. Gould, patented 5 April 1988
2.0*1013 positions
Jaap's page
Russian Gripple

Port to Port
Triple Cross
Ferdinand Lammertink
Pat. Aug 6 1996
5.9*109 positions
Jaap's page

Magic Sphere
Rotos
Jaap's page
Magic Cross (Zauberkreuz)

Flip Side - Thinkfun
Swissmad
369,600
[Jaap's page]
Tsukuda's Square / "it"

Rubik's Fifteen
Binary Bisect 5 - Doug Engel
Palette 7 - Doug Engel

Elemental: Neon (aka Biohazard) #051, designed and made by David Litwin

Uriblock aka Mixbox
The above is a custom version purchased at IPP28 in Prague.


Tri-Trick
Super Brain Spinner, from FoxMind
DieN Logical Toys
One Circle Two Circles, designed, made, and exchanged at IPP32 by Diniar Namdarian
Overlapping Plates

Mind Lock
3-Level Puzzle
Dollar Tree
Jushbox

Here are some interesting sites: