









 The iconic pattern/silhouette puzzle is Tangrams (Tan-Grams).
The Tangram is a special type of dissection puzzle.
It is hugely popular and there is a wealth of information available about it on the Web.
It consists of a square divided into seven pieces.
The first problem is to construct the square from the pieces.
The difference between this type of puzzle and simple dissections, however,
is that Tangram puzzles are accompanied by booklets or cards
depicting various forms, often of geometric or stylized organic figures,
that are to be modeled in two dimensions with the available pieces.
The problem figures are shown in silhouette without revealing the internal borders of the individual pieces.
The designs can be quite elegant and some can be challenging to properly model.
If the puzzle doesn't come with problem silhouettes, it's a mere dissection.
The iconic pattern/silhouette puzzle is Tangrams (Tan-Grams).
The Tangram is a special type of dissection puzzle.
It is hugely popular and there is a wealth of information available about it on the Web.
It consists of a square divided into seven pieces.
The first problem is to construct the square from the pieces.
The difference between this type of puzzle and simple dissections, however,
is that Tangram puzzles are accompanied by booklets or cards
depicting various forms, often of geometric or stylized organic figures,
that are to be modeled in two dimensions with the available pieces.
The problem figures are shown in silhouette without revealing the internal borders of the individual pieces.
The designs can be quite elegant and some can be challenging to properly model.
If the puzzle doesn't come with problem silhouettes, it's a mere dissection.
Jurgen Koeller's site has a nice section devoted to Tangrams, and shows some popular variants. Also check out the Tangraphy page at Ito Puzzle Land.
 Many sets have been produced, some dating back more than a century.
Tangoes is a modern version.
Tangrams probably originated in China in the late 1700's or early 1800's, not thousands of years ago as some have claimed.
However, possibly the oldest known dissection puzzle, the "Loculus of Archimedes" or "Ostomachion" was written about
in the 3rd century B.C.
Read more about the Ostomachion below in my notes on the Lokulus puzzle.
Tangrams was the first real puzzle craze to sweep Europe and America, from about 1815 onwards to 1822 or so.
Ivory
sets
from China are particularly valuable.
In Chinese, Tangrams are known as "Chi-Chiao" - "The Seven Clever Pieces."
Many sets have been produced, some dating back more than a century.
Tangoes is a modern version.
Tangrams probably originated in China in the late 1700's or early 1800's, not thousands of years ago as some have claimed.
However, possibly the oldest known dissection puzzle, the "Loculus of Archimedes" or "Ostomachion" was written about
in the 3rd century B.C.
Read more about the Ostomachion below in my notes on the Lokulus puzzle.
Tangrams was the first real puzzle craze to sweep Europe and America, from about 1815 onwards to 1822 or so.
Ivory
sets
from China are particularly valuable.
In Chinese, Tangrams are known as "Chi-Chiao" - "The Seven Clever Pieces."
Any geometric shape can be dissected into pieces, and the pieces re-arranged to form fanciful figures. You can make up your own problems by inventing a pretty figure, tracing around the completed figure and then challenging others to reproduce it. Perhaps no other company has expanded on the idea more than the German F. Adolph Richter and Company, which began producing a line of "Anchor Stone Puzzles" in 1882. (They also made sets of building blocks, discussed on George Hardy's site.) Richter made blocks from a mixture of Kaolin clay, sand, and linseed oil, based on a formula patented by Otto Lilienthal. Most of the Anchor puzzles are dissected rectangles. A team of artists came up with the hundreds of problem silhouettes.


 Jerry Slocum
has written a book all about the familiar Tangram puzzle and its surprising history, and more recently issued a
book all about the Anchor puzzles.
The noted American puzzle inventor Sam Loyd
published a book of over 650 problems called "The Eigth Book of Tan Part I" in 1903,
and concocted a bogus backstory for the puzzle.
Slocum debunks Loyd's claims and explores the true history of the Tangram puzzle,
based on globe-spanning research.
Slocum includes over 1700 Tangram problems compiled from several sources around the world and from different periods.
By the late 1800's there were at least 36 puzzles in the Anchor lineup.
Slocum and Botermans discuss the complete lineup in "Puzzles Old and New" on pp.27-33.
Stewart Coffin examines them in his book
The Puzzling World of Polyhedral Dissections.
I list them in the table below, and show pictures I have been able to find.
The Anchor puzzles are very collectible, if you're interested in this category.
I own only those puzzles listed in bold.
Some of the designs have proven to be broadly popular -
I highlight those using a light background color.
Jerry Slocum
has written a book all about the familiar Tangram puzzle and its surprising history, and more recently issued a
book all about the Anchor puzzles.
The noted American puzzle inventor Sam Loyd
published a book of over 650 problems called "The Eigth Book of Tan Part I" in 1903,
and concocted a bogus backstory for the puzzle.
Slocum debunks Loyd's claims and explores the true history of the Tangram puzzle,
based on globe-spanning research.
Slocum includes over 1700 Tangram problems compiled from several sources around the world and from different periods.
By the late 1800's there were at least 36 puzzles in the Anchor lineup.
Slocum and Botermans discuss the complete lineup in "Puzzles Old and New" on pp.27-33.
Stewart Coffin examines them in his book
The Puzzling World of Polyhedral Dissections.
I list them in the table below, and show pictures I have been able to find.
The Anchor puzzles are very collectible, if you're interested in this category.
I own only those puzzles listed in bold.
Some of the designs have proven to be broadly popular -
I highlight those using a light background color.
The German company Anker Steinbaukasten GmbH still exists today and still sells building sets and puzzles. You can buy new Anchor puzzles at:

 No. 1 Alle Neune [New version available.] |

No. 2 Blitzableiter |


No. 3 Ei des Columbus [New version available.] I have a metal version from Thinkfun called the Scrambled Egg. |

No. 4 Geduldprüfer |

No. 5 Grillentöter |

 No. 6 Herzratsel I have a modern plastic version, Kohner's Tormentor. [New version available.] |



No. 7 Kobold Note: the Devil puzzle in wood offered by B&P is identical. |



No. 8 Kopfzerbrecher This is the "classic" Tangram set. I have an Anchor version in an old blue box, and a copy offered a while ago by Bits and Pieces. I also have a modern plastic version, Kohner's Pythagoras (not to be confused with Anchor's #12). [New version available.] |




No. 9 Kreisratsel I also have a copy offered a while ago by Bits and Pieces. [New version available.] |



No. 10 Kreuzspiel The Lucky Puzzle from Japan is a plastic version. Kohner's Voodoo is another plastic version. |

 No. 11 Nicht zu Hitzig |

 

No. 12 Pythagoras Zany, copyright 1939 by the Martel Co. of N.Y. is a copy. The set includes seven green wooden pieces from which one can construct a square approx. 70mm on a side. A "Puzzle Book No. 1" contains 138 problems, and solutions are shown in the corresponding "Answer Book No. 1." |

 No. 13 Qualgeist
|

 No. 14 Ruhig Blut |



No. 15 Sphinx Lott's Stone Puzzle is a copy. |

 No. 16 Wunderei (Same pieces as No. 3; different problems.) |

 No. 17 Zornbrecher [New version available.] |
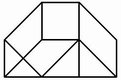 No. 18 Archimedes Not the Stomachion. |
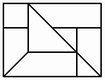 No. 19 Ende Gut, Alles Gut |
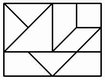 No. 20 Pass Auf |
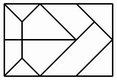 No. 21 Eile mit Weile |
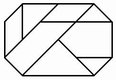 No. 22 Sorgenbrecher |
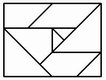 No. 23 Kopernikus |
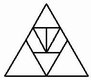 No. 24 Pyramide |

 No. 25 Nur Mut I have a recent copy of Nur Mut. |

No. 26 Bose Sieben |

 No. 27 Ritze Ratze |

No. 28 Frisch Gewagt |

No. 29 Zeitvertreiber |

No. 30 Zeppelin |
 No. 31 Kiebitz-Ei |
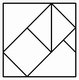 No. 32 Wer Wegt Gewinnt |
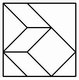 No. 33 Fur Kluge Leute |
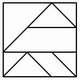 No. 34 Hexenmeister |

 No. 35 Teufelchen |

 No. 36 Heureka |

 No. ? Schutzengraben |

 No. ? Zoologischer Garten (Same pieces as Schutzengraben; different problems.) |

 No. ? Picco (There are 3 different Picco puzzles.) |

 No. ? Stern Raadsel |

 No. ? Blumen Spiel |
|||
 Vexier Mosaik 1 (There are 4 different Vexier Mosaik puzzles.) |

 Vexier Mosaik 2 |

 Vexier Mosaik 3 |
 Vexier Mosaik 4 |
[22]


[1]
Kohner (or its Tryne Game Division) has offered some sets:
[6]

Nob Devil |


 Here are two versions of the Elzzup puzzle by Wm. F. Drueke. |

Mental Aerobics - by Maple Landmark. A tangram set, equivalent to the Anchor #26 "Bose Sieben." Purchased during a visit to the Vermont Country Store. |
 This is the Tangrams Box by James Lyon. |
 Binary Arts Tangram |
 Q-Pak |

Jaymar Jigso |

Barnes & Noble Tangram set |

Spears Superpuzzle |

Heart Tangram by Pussy Puzzles of Germany |
||

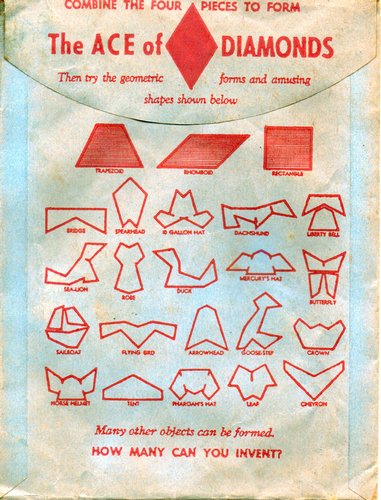
 This is a vintage Ace of Diamonds puzzle. It is a four-piece dissection of a diamond shape.
The four pieces can also be used to make several other shapes as shown on the back of the envelope, including a rectangle
(but not a square) and the interesting "Goose-Step," so this puzzle
is a tangram-type as well.
This is a vintage Ace of Diamonds puzzle. It is a four-piece dissection of a diamond shape.
The four pieces can also be used to make several other shapes as shown on the back of the envelope, including a rectangle
(but not a square) and the interesting "Goose-Step," so this puzzle
is a tangram-type as well.
|
||


Hikimi Longram (I am missing the booklet of shapes.) |
||


The F - Nob Puzzle Series 1987 A nice wooden tangram-style puzzle. The first challenge, to reassemble the dissected letter F, is quite enjoyable. |
||


Cross - Hikimi NOB series |
||

Euclid - Hikimi NOB series |

Octa - Hikimi NOB series |


Nob Gem puzzle - one of a series of tangram-type puzzles, from Japan, copyright 1994. |
[18] (NOTE I have two versions of Elzzup.)